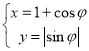题目内容
【题目】如图,椭圆W:![]() 的焦距与椭圆Ω:
的焦距与椭圆Ω:![]() +y2=1的短轴长相等,且W与Ω的长轴长相等,这两个椭圆的在第一象限的交点为A,直线l经过Ω在y轴正半轴上的顶点B且与直线OA(O为坐标原点)垂直,l与Ω的另一个交点为C,l与W交于M,N两点.
+y2=1的短轴长相等,且W与Ω的长轴长相等,这两个椭圆的在第一象限的交点为A,直线l经过Ω在y轴正半轴上的顶点B且与直线OA(O为坐标原点)垂直,l与Ω的另一个交点为C,l与W交于M,N两点.

(1)求W的标准方程:
(2)求![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由题意可得![]() ,求出a2,b2,即可得到W的标准方程,
,求出a2,b2,即可得到W的标准方程,
(2)先求出直线l的方程为y=﹣3x+1,分别与椭圆W和椭圆Ω,联立方程组,求出BC和MN,比较即可
(1)由题意可得![]() ,
,
∴![]()
故W的标准方程为![]() .
.
(2)联立 得
得
∴![]() ,
,
∴![]() ,
,
易知B(0,1),
∴l的方程为y=﹣3x+1.
联立 ,得37x2﹣24x=0,
,得37x2﹣24x=0,
∴x=0或![]() ,
,
∴![]() ,
,
联立 ,得31x2﹣18x﹣9=0,
,得31x2﹣18x﹣9=0,
设M(x1,y1),N(x2,y2),
则![]() ,
,![]() ,
,
∴![]() ,
,
故![]() .
.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目