题目内容
设F1,F2分别是椭圆C: +
+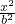 =1(a>b>0)的焦点,若椭圆C上存在点P,使线段PF1的垂直平分线过点F2,则椭圆离心率的取值范围是
=1(a>b>0)的焦点,若椭圆C上存在点P,使线段PF1的垂直平分线过点F2,则椭圆离心率的取值范围是
- A.(0,
 ]
] - B.(
 ,
, )
) - C.[
 ,1)
,1) - D.[
 ,
, )
)
C
分析:若椭圆C上存在点P,使线段PF1的垂直平分线过点F2,只需以点F2为圆心2c为半径的圆与椭圆有交点即可.
解答:因为设F1,F2分别是椭圆C: +
+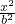 =1(a>b>0)的焦点,若椭圆C上存在点P,使线段PF1的垂直平分线过点F2,
=1(a>b>0)的焦点,若椭圆C上存在点P,使线段PF1的垂直平分线过点F2,
则以点F2为圆心2c为半径的圆与椭圆有交点,由椭圆的性质可知只需满足a-c≤2c,解得 ,所以椭圆离心率的取值范围是[
,所以椭圆离心率的取值范围是[ ,1).
,1).
故选C.
点评:本题考查椭圆的简单性质的应用,考查转化是的应用,以及计算能力.
分析:若椭圆C上存在点P,使线段PF1的垂直平分线过点F2,只需以点F2为圆心2c为半径的圆与椭圆有交点即可.
解答:因为设F1,F2分别是椭圆C:
 +
+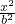 =1(a>b>0)的焦点,若椭圆C上存在点P,使线段PF1的垂直平分线过点F2,
=1(a>b>0)的焦点,若椭圆C上存在点P,使线段PF1的垂直平分线过点F2,则以点F2为圆心2c为半径的圆与椭圆有交点,由椭圆的性质可知只需满足a-c≤2c,解得
 ,所以椭圆离心率的取值范围是[
,所以椭圆离心率的取值范围是[ ,1).
,1).故选C.
点评:本题考查椭圆的简单性质的应用,考查转化是的应用,以及计算能力.

练习册系列答案
相关题目