题目内容
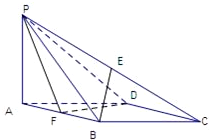
已知AB与CD为异面线段，CD?平面α，AB∥α，M、N分别是线段AC与BD的中点，求证：MN∥平面α．
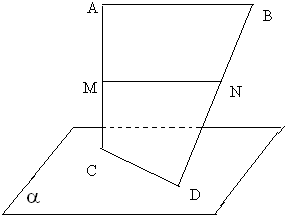
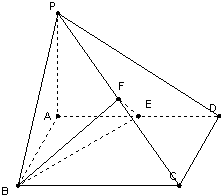
证明：如图：根据已知AB与CD为异面线段，可得A、B、C、D不共面．
连结AD，并取AD中点E，可得M、N、E不共线，故M、N、E确定一个平面．
∵N是BD的中点，∴NE∥AB．
又AB∥α，∴NE∥α．
∵M是AC的中点，∴ME∥CD，再由CD?平面α，ME不在平面α内，可得ME∥α，
∵ME∩NE=E，∴平面MEN∥平面α，∴MN∥平面α．
连结AD，并取AD中点E，可得M、N、E不共线，故M、N、E确定一个平面．
∵N是BD的中点，∴NE∥AB．
又AB∥α，∴NE∥α．
∵M是AC的中点，∴ME∥CD，再由CD?平面α，ME不在平面α内，可得ME∥α，
∵ME∩NE=E，∴平面MEN∥平面α，∴MN∥平面α．
练习册系列答案
华东师大版一课一练系列答案
孟建平名校考卷系列答案
相关题目
