题目内容
已知函数f(x)=x3-3ax+2(其中a为常数)有极大值18.(Ⅰ)求a的值;
(Ⅱ)若曲线y=f(x)过原点的切线与函数g(x)=b-lnx的图象有两个交点,试求b的取值范围.
【答案】分析:(Ⅰ)用导数求出函数的极大值点,根据极大值为18列出方程即可解得.
(Ⅱ)求出切线方程,利用数形结合思想把图象的交点个数转化为函数最值问题解决.
解答:解:(Ⅰ)f′(x)=3x2-3a,又函数f(x)有极大值,
∴令f′(x)>0,得x<-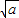 或x
或x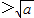 ,
,
∴f(x)在(-∞,-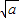 ),(
),(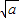 ,+∞)上递增,在(-
,+∞)上递增,在(-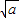 ,
,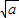 )上递减,
)上递减,
∴f(x)极大值=f(-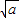 )=18,解得a=4.
)=18,解得a=4.
(Ⅱ)设切点(x,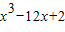 ),则切线斜率k=f′(x)=
),则切线斜率k=f′(x)=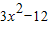 ,
,
所以切线方程为y-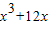 -2=(
-2=(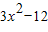 )(x-x),
)(x-x),
将原点坐标代入得x=1,所以k=-9.
切线方程为y=-9x.
由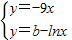 得lnx-9x-b=0.
得lnx-9x-b=0.
设h(x)=lnx-9x-b,
则令h′(x)=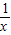 -9=
-9=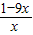 >0,得0<x<
>0,得0<x< ,
,
所以h(x)在(0, )上递增,在(
)上递增,在( ,+∞)上递减,
,+∞)上递减,
所以h(x)最大值=h( )=-ln9-1-b.
)=-ln9-1-b.
若lnx-9x-b=0有两个解,则h(x)最大值>0,
得b<-ln9-1.
点评:本题考查了利用导数研究函数的极值、最值问题,考查了用所学知识解决问题的能力,注意数形结合思想在本题中的运用.
(Ⅱ)求出切线方程,利用数形结合思想把图象的交点个数转化为函数最值问题解决.
解答:解:(Ⅰ)f′(x)=3x2-3a,又函数f(x)有极大值,
∴令f′(x)>0,得x<-
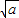 或x
或x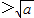 ,
,∴f(x)在(-∞,-
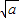 ),(
),(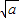 ,+∞)上递增,在(-
,+∞)上递增,在(-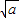 ,
,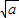 )上递减,
)上递减,∴f(x)极大值=f(-
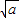 )=18,解得a=4.
)=18,解得a=4.(Ⅱ)设切点(x,
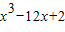 ),则切线斜率k=f′(x)=
),则切线斜率k=f′(x)=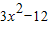 ,
,所以切线方程为y-
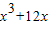 -2=(
-2=(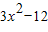 )(x-x),
)(x-x),将原点坐标代入得x=1,所以k=-9.
切线方程为y=-9x.
由
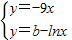 得lnx-9x-b=0.
得lnx-9x-b=0.设h(x)=lnx-9x-b,
则令h′(x)=
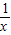 -9=
-9=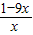 >0,得0<x<
>0,得0<x< ,
,所以h(x)在(0,
 )上递增,在(
)上递增,在( ,+∞)上递减,
,+∞)上递减,所以h(x)最大值=h(
 )=-ln9-1-b.
)=-ln9-1-b.若lnx-9x-b=0有两个解,则h(x)最大值>0,
得b<-ln9-1.
点评:本题考查了利用导数研究函数的极值、最值问题,考查了用所学知识解决问题的能力,注意数形结合思想在本题中的运用.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|