题目内容
18.若不等式|x-2|+|x-3|>|k-1|对任意的x∈R恒成立,则实数k的取值范围是( )| A. | [2,4] | B. | [0,2] | C. | (2,4) | D. | (0,2) |
分析 令f(x)=|x-2|+|x-3|,化成分段函数,求出f(x)的最小值fmin(x),令fmin(x)>|k-1|解出k的范围即可.
解答 解:设f(x)=|x-2|+|x-3|,则f(x)=$\left\{\begin{array}{l}{5-2x,x≤2}\\{1,2<x<3}\\{2x-5,x≥3}\end{array}\right.$,
∴f(x)的最小值为1,
∵不等式|x-2|+|x-3|>|k-1|对任意的x∈R恒成立,
∴1>|k-1|,解得0<k<2.
故选:D.
点评 本题考查了分段函数的最值计算,函数最值与函数恒成立研究,属于基础题.

练习册系列答案
相关题目
13.已知命题P:存在x∈R,mx2+1≤1,q对任意x∈R,x2+mx+1≥0,若p∨(¬q)为假命题,则实数m的取值范围是( )
| A. | (-∞,0)∪(2,+∞) | B. | (0,2] | C. | [0,2] | D. | Φ |
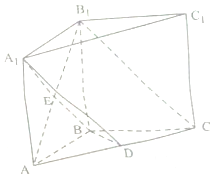 如图,在直三棱柱ABC-A1B1C1中,AB=BC=BB1,AB1∩A1B=E,D为AC上的点,B1C∥平面A1BD.
如图,在直三棱柱ABC-A1B1C1中,AB=BC=BB1,AB1∩A1B=E,D为AC上的点,B1C∥平面A1BD. 已知函数f(x)=6sinωxcosωx-8cos2ωx+3(ω>0),y=f(x)+1的部分图象如图所示,且f(x0)=4,则f(x0+1)=( )
已知函数f(x)=6sinωxcosωx-8cos2ωx+3(ω>0),y=f(x)+1的部分图象如图所示,且f(x0)=4,则f(x0+1)=( )