题目内容
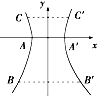 热电厂的冷却塔的外形是双曲线型,是双曲线的一部分绕其虚轴所在直线旋转所成的曲面,它的最小直径是24m,上口直径是26m,下口直径是50m,高是55m,建立如图所示的直角坐标系,求此双曲线的方程(精确到1m).
热电厂的冷却塔的外形是双曲线型,是双曲线的一部分绕其虚轴所在直线旋转所成的曲面,它的最小直径是24m,上口直径是26m,下口直径是50m,高是55m,建立如图所示的直角坐标系,求此双曲线的方程(精确到1m).分析:设双曲线的标准方程,利用条件确定a,b.
解答:解:设双曲线的标准方程为
-
=1(a>0,b>0),
则由题意知AA'=2a=24,所以a=12.
点B,C的横坐标分别为-25,-13.则设点B,C的坐标为(-25,y1),(-13,y2),(y1<0,y2>0),
所以
,解得y1=-
b,y2=
,
又因为塔高55米,则y2-y1=55,即
+
b=55,解答b≈25,
故所求的双曲线的方程为
-
=1.
| x2 |
| a2 |
| y2 |
| b2 |
则由题意知AA'=2a=24,所以a=12.
点B,C的横坐标分别为-25,-13.则设点B,C的坐标为(-25,y1),(-13,y2),(y1<0,y2>0),
所以
|
| ||
| 12 |
| 5b |
| 12 |
又因为塔高55米,则y2-y1=55,即
| 5b |
| 12 |
| ||
| 12 |
故所求的双曲线的方程为
| x2 |
| 144 |
| y2 |
| 625 |
点评:本题主要考查双曲线方程的应用,运算量较大.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
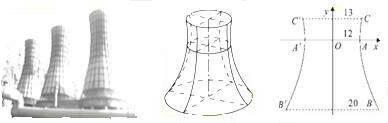

 ,试求冷却塔的高应当设计为多少?
,试求冷却塔的高应当设计为多少?
 ,试求冷却塔的高应当设计为多少?
,试求冷却塔的高应当设计为多少?