题目内容
已知函数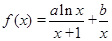 ,曲线
,曲线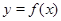 在点
在点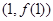 处的切线方程为
处的切线方程为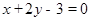 。
。
(Ⅰ)求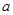 、
、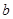 的值;
的值;
(Ⅱ)如果当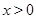 ,且
,且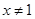 时,
时,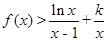 ,求
,求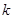 的取值范围
的取值范围
【答案】
(1) (2)
(2)
【解析】(I)可求出点(1,1)在函数f(x)的图像上,再根据 ,建立两个关于a,b方程,解方程组即可求出a,b的值。
,建立两个关于a,b方程,解方程组即可求出a,b的值。
(II)  可得
可得
 ,再设然后对
,再设然后对 求导讨论k研究其单调性即可。
求导讨论k研究其单调性即可。
解:(Ⅰ) ,由题意知:
,由题意知: 即
即
 ----4分
----4分
(Ⅱ)由(Ⅰ)知 ,所以,
,所以,


设 则,
则, ------6分
------6分
⑴如果 ,由
,由 知,当
知,当 时,
时, ,而
,而
故,由当 得:
得:
从而,当 时,
时, 即
即 ------------9分
------------9分
⑵如果 ,则当,
,则当, 时,
时,
而 ;
; 得:
得: 与题设矛盾; ------------11分
与题设矛盾; ------------11分
 ⑶如果
⑶如果 ,那么,因为
,那么,因为 而
而 ,
, 时,由
时,由 得:
得: 与题设矛盾;
与题设矛盾;
综合以上情况可得:

练习册系列答案
相关题目
 ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为 ,
, 的值
的值 时,
时,
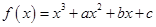 ,曲线
,曲线 在点
在点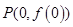 处的切线是
处的切线是 :
:
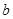 ,
,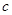 的值;
的值;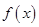 在
在 上单调递增,求
上单调递增,求 的取值范围
的取值范围 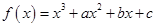 ,曲线
,曲线 在点
在点 处的切线是
处的切线是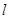 :
: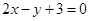
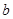 ,
,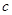 的值;
的值;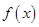 在
在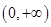 上单调递增,求
上单调递增,求 的取值范围
的取值范围