Question

某班共有学生50名，其中参加数学课外小组的学生有22人，参加物理课外小组的学生有18人，同时参加数学、物理两个课外小组的有13人，问：

(1)数学和物理两个小组至少参加一个的学生有多少人？

(2)数学和物理两个课外小组都不参加的学生有多少人？

Answer 1

答案：
解析：

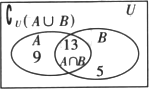
解法1：设全集U＝{某班学生}，A＝{该班参加数学小组的学生}，B＝{该班参加物理课外小组的学生}，则知U中有50个元素，A中有22个元素，B中有18个元素，A∩B有13个元素，A∩B＝{该班只参加数学课外小组的学生}，有22－13＝9个元素，B∩A＝{该班只参加物理课外小组的学生}，有元素18－13＝5个，A∪B＝{数学和物理两个小组至少参加一个的学生}，有元素9＋13＋5＝27个，(A∪B)中含有50－27＝23个元素． 　　∴(1)数学和物理两小组至少参加一个小组的学生有27人． 　　(2)数学和物理都不参加的学生有23人． 　　解法2：利用Venn图来解，如下图，从图上可直接看出上面(1)(2)的结果数学和物理两个小组至少参加一个的有9＋13＋5＝27人，数学和物理都不参加的有50－27＝23人． 　　思想方法小结：解法1是采用分析法，解法2是采用数形结合．

提示：

将应用问题转化为数学的集合问题，进行集合的交、并、补集运算．