题目内容
已知椭圆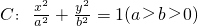 的两个焦点分别为F1(-1,0),F2(1,0),长半轴长为
的两个焦点分别为F1(-1,0),F2(1,0),长半轴长为 .
.
(1)(i)求椭圆C的方程;
(ii)类比结论“过圆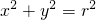 上任一点(x0,y0)的切线方程是
上任一点(x0,y0)的切线方程是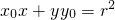 ”,归纳得出:过椭圆
”,归纳得出:过椭圆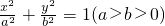 上任一点(x0,y0)的切线方程是________;
上任一点(x0,y0)的切线方程是________;
(2)设M,N是直线x=2上的两个点,若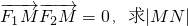 的最小值.
的最小值.
解:(1)(i)由焦点坐标可知c=1,长半轴长为 ,可知,a=
,可知,a= ,所以b=1,
,所以b=1,
所以椭圆C的方程为 .
.
(ii)过圆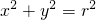 上任一点(x0,y0)的切线方程是
上任一点(x0,y0)的切线方程是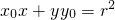 ,
,
过椭圆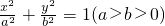 上任一点(x0,y0)的切线方程是:
上任一点(x0,y0)的切线方程是: .
.
(2)∵M,N是直线x=2上的两个点,
∴设m(2,y1),N(2,y2),(不妨y1>y2).
∵ ,
,
∴(3,y1)•(1,y2)=0,
即3+y1y2=0,由于y1>y2.所以
y1>0,y2<0,
∴|MN|=y1-y2=y1+
 ,
,
当且仅当y1= ,y2=-
,y2=- ,时取等号.
,时取等号.
故|MN|的最小值为:2 .
.
故答案为:(ii) .
.
分析:(1)直接利用椭圆的焦点坐标与长半轴,求出b,然后求解椭圆的方程.
(2)(i)直接类比圆的切线方程,写出椭圆的切线方程即可.
(ii)设m(2,y1),N(2,y2),通过向量的数量积,推出y1,y2的关系,求出|MN|的表达式,利用基本不等式求出最小值即可.
点评:本题考查椭圆的标准方程的求法,向量的数量积,基本不等式的应用,考查计算能力,转化思想的应用.
 ,可知,a=
,可知,a= ,所以b=1,
,所以b=1,所以椭圆C的方程为
 .
.(ii)过圆
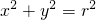 上任一点(x0,y0)的切线方程是
上任一点(x0,y0)的切线方程是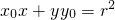 ,
,过椭圆
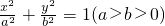 上任一点(x0,y0)的切线方程是:
上任一点(x0,y0)的切线方程是: .
.(2)∵M,N是直线x=2上的两个点,
∴设m(2,y1),N(2,y2),(不妨y1>y2).
∵
 ,
,∴(3,y1)•(1,y2)=0,
即3+y1y2=0,由于y1>y2.所以
y1>0,y2<0,
∴|MN|=y1-y2=y1+

 ,
,当且仅当y1=
 ,y2=-
,y2=- ,时取等号.
,时取等号.故|MN|的最小值为:2
 .
.故答案为:(ii)
 .
.分析:(1)直接利用椭圆的焦点坐标与长半轴,求出b,然后求解椭圆的方程.
(2)(i)直接类比圆的切线方程,写出椭圆的切线方程即可.
(ii)设m(2,y1),N(2,y2),通过向量的数量积,推出y1,y2的关系,求出|MN|的表达式,利用基本不等式求出最小值即可.
点评:本题考查椭圆的标准方程的求法,向量的数量积,基本不等式的应用,考查计算能力,转化思想的应用.

练习册系列答案
相关题目
 :
:
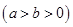 ,称圆心在坐标原点
,称圆心在坐标原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 ,椭圆
,椭圆 满足
满足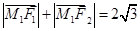 .
.
 作直线
作直线 ,使得直线
,使得直线 .求出
.求出 的值.
的值. :
:
 ,称圆心在坐标原点
,称圆心在坐标原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 ,椭圆
,椭圆 满足
满足 .
. (0,
(0,  )
) ,使得过点
,使得过点 与椭圆
与椭圆 .若存在,请求出
.若存在,请求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。 :
:
 ,称圆心在坐标原点
,称圆心在坐标原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 ,椭圆
,椭圆 满足
满足 .
.
 作直线
作直线 ,使得直线
,使得直线 .求出
.求出 的值.
的值.