题目内容
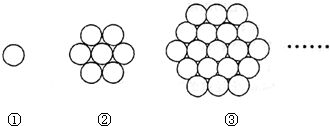
如图①，②，③，…是由花盆摆成的图案，根据图中花盆摆放的规律，猜想第n个图形中花盆的盆数an=
3n2-3n+1
3n2-3n+1
．分析：观察图形很容易看出第一个图象由一盆花，第二个图形比第一个图形多放了6盆，第三个图形比第二个图形多放了2×6盆，可得后面图形花盆数前面图形花盆数存在关系，an-an-1=6×（n-1），利用累加法可得答案．
解答：解：由图知a1=1
a2-a1=6=6×（2-1），
a3-a2=12=6×（3-1），
…
an-an-1=6×（n-1），
∴an=1+6+12+…+6×（n-1）=1+
=3n2-3n+1
故答案为3n2-3n+1
a2-a1=6=6×（2-1），
a3-a2=12=6×（3-1），
…
an-an-1=6×（n-1），
∴an=1+6+12+…+6×（n-1）=1+
| 6n(n-1) |
| 2 |
故答案为3n2-3n+1
点评：本题是一道找规律的题目，这类题型在中考中经常出现．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．
练习册系列答案
相关题目
（理科）如图所示的几何体底面ABC是直角三角形，∠CAB=90°，AC=4，AB=4，DA，EC，FB均垂直于底面ABC，且CE=3，BF=1，AD=2，点G为棱EF上的一点，且
如图，正四棱锥 （底面是正方形，顶点在底面的射影是底面的中心）P-ABCD的底面边长为6cm，侧棱长为5cm，则它的正视图的面积等于（ ）
如图，长方体ABCD-A1B1C1D1中，P是线段AC的中点．
一个多面体是由正方体割去两个三棱锥得到的，其正视图、侧视图、府视图均是边长为2的正方形，如图所示，该多面体的表面积是（ ）
已知四棱锥P-ABCD中，点M是PC的中点，点E是AB上的一个动点，且该四棱锥的三视图如图所示，其中正视图和侧视图是直角三角形．