题目内容
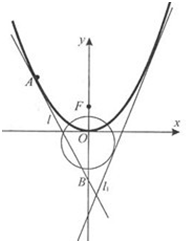 如图,已知直线
如图,已知直线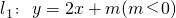 与抛物线
与抛物线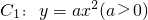 和圆
和圆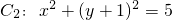 都相切,F是C1的焦点.
都相切,F是C1的焦点.
(1)求m与a的值;
(2)设A是C1上的一动点,以A为切点作抛物线C1的切线l,直线l交y轴于点B,以FA,FB为邻边作平行四边形FAMB,证明:点M在一条定直线上.
(1)解:由已知,圆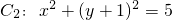 的圆心(0,-1),
的圆心(0,-1),
圆心到直线l1:y=2x+m的距离 ,解得m=-6(m=4舍去),…(3分)
,解得m=-6(m=4舍去),…(3分)
设l1与抛物线的相切点为A0(x0,y0),得2ax0=2,∴ ,
,
代入直线方程得: ,∴
,∴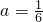 ,
,
所以m=-6,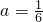 …(6分)
…(6分)
(2)证明:由(1)知抛物线C1方程为 ,焦点
,焦点 ,
,
设 ,由(1)知以A为切线l的方程为
,由(1)知以A为切线l的方程为 ,…(8分)
,…(8分)
令x=0,得切线l交y轴的B点坐标为(0, ),
),
所以 =(x1,
=(x1,
 -
- ),
), =(0,-
=(0,-
 -
- ),…(10分)
),…(10分)
∵四边形FAMB是以FA,FB为邻边的平行四边形,
∴ =(x1,-3)…(13分)
=(x1,-3)…(13分)
因为F是定点 ,所以点M在定直线
,所以点M在定直线 上. …(15分)
上. …(15分)
分析:(1)利用直线与圆相切,可得圆心到直线l1:y=2x+m的距离等于半径,从而可求m的值;设l1与抛物线的相切点为A0(x0,y0),求得切点坐标,代入直线方程,即可求得a的值;
(2)设 ,由(1)知以A为切线l的方程为
,由(1)知以A为切线l的方程为 ,从而可得切线l交y轴的B点坐标,利用四边形FAMB是以FA,FB为邻边的平行四边形,可得
,从而可得切线l交y轴的B点坐标,利用四边形FAMB是以FA,FB为邻边的平行四边形,可得 ,由此可证结论.
,由此可证结论.
点评:本题考查直线与圆,直线与抛物线的位置关系,考查向量知识的运用,解题的关键是确定切线方程,属于中档题.
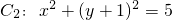 的圆心(0,-1),
的圆心(0,-1),圆心到直线l1:y=2x+m的距离
 ,解得m=-6(m=4舍去),…(3分)
,解得m=-6(m=4舍去),…(3分)设l1与抛物线的相切点为A0(x0,y0),得2ax0=2,∴
 ,
,代入直线方程得:
 ,∴
,∴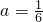 ,
,所以m=-6,
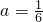 …(6分)
…(6分)(2)证明:由(1)知抛物线C1方程为
 ,焦点
,焦点 ,
,设
 ,由(1)知以A为切线l的方程为
,由(1)知以A为切线l的方程为 ,…(8分)
,…(8分)令x=0,得切线l交y轴的B点坐标为(0,
 ),
),所以
 =(x1,
=(x1,
 -
- ),
), =(0,-
=(0,-
 -
- ),…(10分)
),…(10分)∵四边形FAMB是以FA,FB为邻边的平行四边形,
∴
 =(x1,-3)…(13分)
=(x1,-3)…(13分)因为F是定点
 ,所以点M在定直线
,所以点M在定直线 上. …(15分)
上. …(15分)分析:(1)利用直线与圆相切,可得圆心到直线l1:y=2x+m的距离等于半径,从而可求m的值;设l1与抛物线的相切点为A0(x0,y0),求得切点坐标,代入直线方程,即可求得a的值;
(2)设
 ,由(1)知以A为切线l的方程为
,由(1)知以A为切线l的方程为 ,从而可得切线l交y轴的B点坐标,利用四边形FAMB是以FA,FB为邻边的平行四边形,可得
,从而可得切线l交y轴的B点坐标,利用四边形FAMB是以FA,FB为邻边的平行四边形,可得 ,由此可证结论.
,由此可证结论.点评:本题考查直线与圆,直线与抛物线的位置关系,考查向量知识的运用,解题的关键是确定切线方程,属于中档题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
22.(本题满分15分)已知抛物线C的顶点在原点,焦点在y轴正半轴上,点 到其准线的距离等于5.
到其准线的距离等于5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)如图,过抛物线C的焦点的直线从左到右依次与抛物线C及圆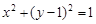 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值;
|
 且
且 交于点M,求
交于点M,求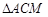 与
与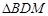 面积之和的最小值.
面积之和的最小值.
(本小题满分15分)
已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5。
(I)求抛物线G的方程;
(II)如图,过抛物线G的焦点的直线依次与抛物线G及圆![]() 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明![]() 为定值;
为定值;
|
 已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5.
已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5.
 到其准线的距离等于5.
到其准线的距离等于5. 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值; 且
且 与
与 面积之和的最小值.
面积之和的最小值.
 |BD|为定值;
|BD|为定值;
