题目内容
设函数f(x)=msinx+3cosx(m∈R),若函数f(x)的图象与直线y=n(n为常数)相邻两个交点的横坐标为x1=
,x2=
(1)求函数f(x)的解析式;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,f(A)=3,a=2,求△ABC周长l的范围.
| π |
| 12 |
| 7π |
| 12 |
(1)求函数f(x)的解析式;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,f(A)=3,a=2,求△ABC周长l的范围.
分析:(1)利用函数f(x)的图象与直线y=n(n为常数)相邻两个交点的横坐标为x1=
,x2=
,建立方程,即可求得m的值,从而可求函数f(x)的解析式;
(2)先确定A的值,再利用余弦定理、基本不等式,即可求△ABC周长l的范围.
| π |
| 12 |
| 7π |
| 12 |
(2)先确定A的值,再利用余弦定理、基本不等式,即可求△ABC周长l的范围.
解答:解:(1)根据题意得:msin
+3cos
=msin
+3cos
=n,
变形得:m=
=
=3
∴f(x)=3
sinx+3cosx;
(2)f(x)=3
sinx+3cosx=6sin(x+
)
∵f(A)=3,∴6sin(A-
)=3,∵A∈(0,π),∴A=
∵a=2,∴4=b2+c2-2bccos
=b2+c2+bc=(b+c)2-bc
∵b+c≥2
,∴0<bc≤
∴
≤(b+c)2-bc<(b+c)2,
∴
≤4<(b+c)2,∴2<b+c≤
∴4<a+b+c≤2+
∴4<l≤2+
| π |
| 12 |
| π |
| 12 |
| 7π |
| 12 |
| 7π |
| 12 |
变形得:m=
3(cos
| ||||
sin
|
-6sin
| ||||
-2cos
|
| 3 |
∴f(x)=3
| 3 |
(2)f(x)=3
| 3 |
| π |
| 6 |
∵f(A)=3,∴6sin(A-
| π |
| 6 |
| π |
| 3 |
∵a=2,∴4=b2+c2-2bccos
| π |
| 3 |
∵b+c≥2
| bc |
| (b+c)2 |
| 4 |
∴
| 3(b+c)2 |
| 4 |
∴
| 3(b+c)2 |
| 4 |
4
| ||
| 3 |
∴4<a+b+c≤2+
4
| ||
| 3 |
∴4<l≤2+
4
| ||
| 3 |
点评:本题考查三角函数的化简,考查余弦定理,考查基本不等式的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
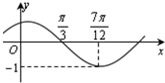 已知函数f(x)=Msin(ωx+φ)(其中
已知函数f(x)=Msin(ωx+φ)(其中