题目内容
6. 一个几何体的三视图如图所示,其中俯视图是一个正方形,则这
一个几何体的三视图如图所示,其中俯视图是一个正方形,则这个几何体的体积是( )
| A. | 64 | B. | 32 | C. | 16 | D. | 8 |
分析 由已知中的三视图,画出几何体的直观图,并判断其形状,进而可得其体积.
解答 解:由已知中的三视图,可得该几何体的直观图如下图所示: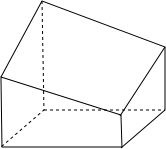
将这样的两个几何体组合在一起,能构成一个棱长为4的正方体,
故几何体的体积V=$\frac{1}{2}$×4×4×4=32,
故选:B.
点评 本题考查的知识点是由三视图求体积和表面积,根据三视图分析出几何体的形状是解答的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
18.一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验,收集数据如下:
(1)画出散点图;
(2)求回归方程;
(3)关于加工零件的个数与加工时间,你能得出什么结论?
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 加工时间y(min) | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
(2)求回归方程;
(3)关于加工零件的个数与加工时间,你能得出什么结论?
1.已知集合A={x|$\frac{1}{x}$<1},B={y|y=2-x-1,x∈R},则A∩B=( )
| A. | ∅ | B. | {x|x>1} | C. | {x|-1<x<0} | D. | {x|-1<x<0或x>1} |
18.已知函数g(x)=$\left\{\begin{array}{l}{\frac{1}{x+1}-3,-1<x≤0}\\{{x}^{2}-3x+2,0<x≤1}\end{array}\right.$,若方程g(x)-mx-m=0有且仅有两个不等的实根,则实数m的取值范围是( )
| A. | (-$\frac{9}{4}$,-2]∪[0,2] | B. | (-$\frac{11}{4}$,-2]∪[0,2] | C. | (-$\frac{9}{4}$,-2]∪[0,2) | D. | (-$\frac{11}{4}$,-2]∪[0,2) |
15.命题“?x∈R,tanx≠1”的否定是( )
| A. | ?x∉R,tanx≠1 | B. | ?x∈R,tanx=1 | C. | ?x∉R,tanx≠1 | D. | ?x∈R,tanx=1 |
 某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为$\frac{80π}{3}$立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>5)千元.设该容器的建造费用为y千元.
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为$\frac{80π}{3}$立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>5)千元.设该容器的建造费用为y千元.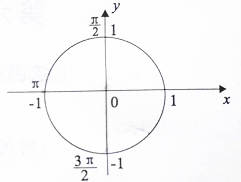 单位圆上三角函数值的集合解释是“角在弧上,值在线上”,试在图中画出α属于第Ⅲ象限的一个正弦值,余弦值.
单位圆上三角函数值的集合解释是“角在弧上,值在线上”,试在图中画出α属于第Ⅲ象限的一个正弦值,余弦值.