题目内容
已知函数 .
.(1)求f(x)的最小正周期;
(2)当x∈[0,π]时,求f(x)的零点;
(3)在给出的坐标系中作出f(x)在一个周期上的简图.
【答案】分析:(1)利用二倍角公式化简函数f(x)的解析式为= ,由此求得周期.
,由此求得周期.
(2)令 ,结合x∈[0,π],求得x的值,即为f(x)的零点.
,结合x∈[0,π],求得x的值,即为f(x)的零点.
(3)用五点法作出函数在一个周期上的简图.
解答: 解:(1)
解:(1) =
= ,
,
所以周期T=2π.---(4分)
(2)令 ,
,
因为x∈[0,π],所以x=π.所以f(x)的零点是x=π.---(3分)
(3)列表:
图象如右.---(3分)
点评:本题主要考查二倍角公式的应用,求函数的零点以及用五点法作函数y=Asin(ωx+φ)的图象,属于中档题.
 ,由此求得周期.
,由此求得周期.(2)令
 ,结合x∈[0,π],求得x的值,即为f(x)的零点.
,结合x∈[0,π],求得x的值,即为f(x)的零点.(3)用五点法作出函数在一个周期上的简图.
解答:
 解:(1)
解:(1) =
= ,
,所以周期T=2π.---(4分)
(2)令
 ,
,因为x∈[0,π],所以x=π.所以f(x)的零点是x=π.---(3分)
(3)列表:
x+ | 0 |  | π |  | 2π |
| x | - |  |  |  |  |
| f(x) |  | 1+ |  | -1+ |  |
点评:本题主要考查二倍角公式的应用,求函数的零点以及用五点法作函数y=Asin(ωx+φ)的图象,属于中档题.

练习册系列答案
相关题目
 .
. .
. 的图象在x轴上方?
的图象在x轴上方? .
. 为f(x)的一个零点,求sin2x的值.
为f(x)的一个零点,求sin2x的值.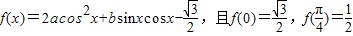 .
. .
. ,求f(x)的最大值和最小值.
,求f(x)的最大值和最小值.