题目内容
已知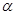 、
、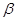 是三次函数
是三次函数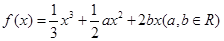 的两个极值点,且
的两个极值点,且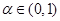 ,
,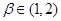 ,则
,则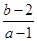 的取值范围是
的取值范围是
A.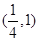 | B.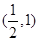 | C.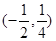 | D.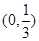 |
A
解析考点:简单线性规划;函数在某点取得极值的条件.
分析:求出导函数,据韦达定理求出α,β与a,b的关系,据α,β的范围求出a,b的范围,画出关于a,b的不等式组的可行域,由图数形结合求出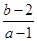 的范围.
的范围.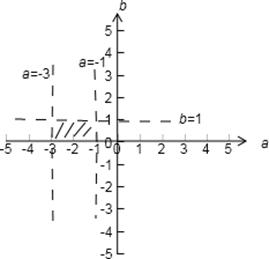
解:f′(x)=x2+ax+2b
∵α,β是f(x)的极值点,
所以α,β是x2+ax+2b=0的两个根
∴α+β=-a,αβ=2b
∵α∈(0,1),β∈(1,2),
∴1<α+β<3,0<αβ<2
∴1<-a<3,0<2b<2
∴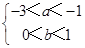
作出不等式组∴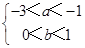 的可行域
的可行域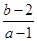 表示可行域中的点与(1,2)连线的斜率
表示可行域中的点与(1,2)连线的斜率
有图知,当当点为(-3,1)和(-1,0)时分别为斜率的最小、最大值
所以此时两直线的斜率分别是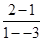 =
=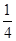 ,
, 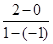 =1
=1
故答案为(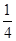 ,1),选A。
,1),选A。

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
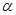 、
、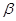 是三次函数
是三次函数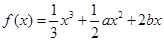 的两个极值点,且
的两个极值点,且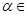 (0、1),
(0、1), (1、2),(
(1、2),(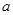 、
、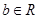 ),则
),则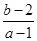 的取值范围是( )
的取值范围是( )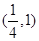 B、
B、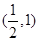 C、
C、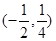 D、
D、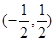
 、
、 是三次函数
是三次函数 的两个极值点,且
的两个极值点,且 ,
, ,则
,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 、
、 是三次函数
是三次函数 的两个极值点,且
的两个极值点,且 ,
, ,则
,则 的取值范围是
的取值范围是 (B)
(B) (C)
(C) (D)
(D)
 的两个极值点,且α∈(0,1),β∈(1,2),求动点(a,b)所在区域面积S.
的两个极值点,且α∈(0,1),β∈(1,2),求动点(a,b)所在区域面积S.