题目内容
(本小题满分14分)
已知圆心 在
在 轴上的圆过点
轴上的圆过点 和
和 .
.
(1)求圆 的方程;
的方程;
(2)求过点 且与圆
且与圆 相切的直线方程;
相切的直线方程;
(3)已知线段 的端点
的端点 的坐标为
的坐标为 ,端点
,端点 在圆
在圆 上运动,求线段
上运动,求线段 的中点N的轨迹.
的中点N的轨迹.
(1) (2)
(2) 或
或 .
.
(3)点N的轨迹是以( ,
, )为圆心,半径为1的圆.
)为圆心,半径为1的圆.
【解析】
试题分析:第一问先通过圆心在弦的中垂线上,从而得出圆心的位置,确定出圆的半径,从而得出圆的方程,第二问涉及到圆的切线方程的求解问题,把握住圆心到直线的距离为半径可得,对于第三问,把握住动点的轨迹方程的求法即可得结果.
试题解析:(1)线段AB的中点坐标为 ,斜率为
,斜率为 (1分)
(1分)
所以线段AB的垂直平分线方程为 ,即为
,即为 . (2分)
. (2分)
令 ,得
,得 ,即圆心为
,即圆心为 . (3分)
. (3分)
由两点间的距离公式,得 . (4分)
. (4分)
∴适合题意的圆 的方程为
的方程为 . (5分)
. (5分)
或:设圆心为 ,由
,由 得
得  (2分)
(2分)
解得a=2,所以圆心为 . (3分)
. (3分)
又半径 . (4分)
. (4分)
所以适合题意的圆 的方程为
的方程为 . (5分)
. (5分)
(2)由(1)知圆 的圆心坐标为
的圆心坐标为 ,半径
,半径
(i)当过点 且与圆
且与圆 相切的直线的斜率不存在时,其切线方程为
相切的直线的斜率不存在时,其切线方程为 .(6分)
.(6分)
(ii)当过点 且与圆
且与圆 相切的直线的斜率存在时,
相切的直线的斜率存在时,
设为 ,则切线方程为
,则切线方程为 . (7分)
. (7分)
由圆心到切线的距离等于半径,得 ,解得
,解得 (8分)
(8分)
所以切线方程为 即
即
因此,过点 且与圆
且与圆 相切的直线方程为
相切的直线方程为 或
或 . (9分)
. (9分)
(3)设点N的坐标为 ,P点的坐标为
,P点的坐标为 .
.
由于Q点的坐标为 且N为PQ的中点,所以
且N为PQ的中点,所以 ,(10分)
,(10分)
于是有 ① (11分)
① (11分)
因为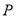 在圆
在圆 上运动,所以有
上运动,所以有 (12分)
(12分)
将①代入上式得 ,即
,即 (13分)
(13分)
所以,点N的轨迹是以( ,
, )为圆心,半径为1的圆. (14分)
)为圆心,半径为1的圆. (14分)
考点:圆的方程,圆的切线,动点的轨迹.

 阅读快车系列答案
阅读快车系列答案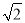 的等腰直角三角形,则该三棱锥的外接球的表面积是( )
的等腰直角三角形,则该三棱锥的外接球的表面积是( )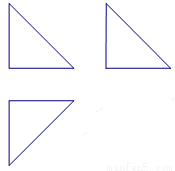
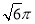 (B)6
(B)6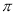 (C)
(C)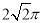 (D)
(D)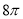
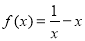 的图像关于( )
的图像关于( )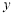 轴对称 B. 直线
轴对称 B. 直线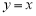 对称 C. 坐标原点对称 D. 直线
对称 C. 坐标原点对称 D. 直线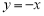 对称
对称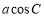 ,
,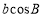 ,
,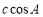 满足
满足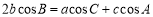 ,若
,若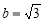 ,则
,则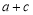 的最大值为
的最大值为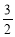 B.3 C.
B.3 C.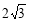 D.9
D.9 R,同时满足条件
R,同时满足条件 和
和 的函数是
的函数是 B.
B. C.
C. D.
D.
 :
: 上,点Q在圆
上,点Q在圆 :
: 上,
上, 的最大值为 .
的最大值为 . 与圆
与圆 相交于A、B两点,则AB的长度等于
相交于A、B两点,则AB的长度等于 C.
C. D.
D.
 的焦点到它的准线的距离等于 .
的焦点到它的准线的距离等于 .