Question

幂函数y=

x

的图象上的点 P_n（t_n²，t_n）（n=1，2，…）与x轴正半轴上的点Q_n及原点O构成一系列正△P_nQ_n-1Q_n（Q₀与O重合），记a_n=|Q_nQ_n-1|
（1）求a₁的值；   
（2）求数列{a_n}的通项公式 a_n；
（3）设S_n为数列{a_n}的前n项和，若对于任意的实数λ∈[0，1]，总存在自然数k，当n≥k时，3S_n-3n+2≥（1-λ）（3a_n-1）恒成立，求k的最小值．

Answer 1

分析：（1）由P₁（t₁²，t₁）（t＞0），知kOP1=

1

t1

=tan

π

3

=

3

，由此能求出a₁的值．
（2）设 P_n（t_n²，t_n），得直线 P_nQ_n-1的方程为：y-t_n=

3

（x-t_n²），故Q_n-1（t_n²-

tn

3

，0），由直线 P_nQ_n的方程为：y-t_n=-

3

（x-t_n²），得 Q_n（t_n²+

tn

3

，0），故t_n²-

tn

3

=t_n-1²+

tn-1

3

，由此能求出a_n．
（3）对于任意的实数λ∈[0，1]，总存在自然数k，当n≥k时，3S_n-3n+2≥（1-λ）（3a_n-1）恒成立，等价于对任意实数 λ∈[0，1]时，（2n-1）λ+n²-4n+3≥0 恒成立．令f （λ）=（2n-1）λ+n²-4n+3，对任意实数 λ∈[0，1]时，

f(0)=n2-4n+3≥0 f(1)=n2-2n+2≥0

，由此能求出k 的最小值．

解答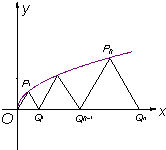：解：（1）∵P₁（t₁²，t₁）（t＞0），…（1分），
∴kOP1=

1

t1

=tan

π

3

=

3

，解得t₁=

3

3

，
∴P₁（

1

3

，

3

3

），a₁=|Q₁Q₀|=|OP₁|=

2

3

．…（5分）
（2）设 P_n（t_n²，t_n），得直线 P_nQ_n-1的方程为：y-t_n=

3

（x-t_n²），
∴Q_n-1（t_n²-

tn

3

，0），
直线 P_nQ_n的方程为：y-t_n=-

3

（x-t_n²），
∴得 Q_n（t_n²+

tn

3

，0）
∴Q_n-1（t_n-1²+

tn-1

3

，0），故t_n²-

tn

3

=t_n-1²+

tn-1

3

，
由 t_n＞0，得t_n-t_n-1=

1

3

∴t_n=t₁+

1

3

（n-1）=

3

3

n．…（8分）
∴Q_n（

1

3

n（n+1），0），Q_n-1（

1

3

n（n-1），0），
∴a_n=|Q_nQ_n-1|=

2

3

n．…（10分）
（3）∵对于任意的实数λ∈[0，1]，总存在自然数k，
当n≥k时，3S_n-3n+2≥（1-λ）（3a_n-1）恒成立，
∴对任意实数λ∈[0，1]时 n²-2n+2≥（1-λ） （2n-1）恒成立，
∴对任意实数 λ∈[0，1]时，（2n-1）λ+n²-4n+3≥0 恒成立．…（12分）
令f （λ）=（2n-1）λ+n²-4n+3，
则 f （λ） 是关于 λ 的一次函数．
∴对任意实数 λ∈[0，1]时，

f(0)=n2-4n+3≥0 f(1)=n2-2n+2≥0

，…（14分）
解得n≥3或n≤1，
又∵n∈N^*，∴k 的最小值为3．…（16分）

点评：本题考查数列与函数的综合运用，综合性强，难度大，具有一定的探索性，对数学思维的要求较高．解题时要认真审题，仔细解答，注意合理地进行等价转化．