题目内容
若公比为c的等比数列{an}的首项a1=1且满足an=
(n=3,4,…).(1)求c的值;
(2)求数列{nan}的前n项和Sn.
分析:(2)c的取值不同Sn的结果不一样,故需讨论.
解:(1)由题设,当n≥3时,an=c2an-2,an-1=can-2,an==
an-2.由题设条件可得an-2≠0,因此c2=
,即2c2-c-1=0.解得c=1或c=-
.
(2)由(1),需要分两种情况讨论.当c=1时,数列{an}是一个常数列,即an=1(n∈N*).这时,数列{nan}的前n项和Sn=1+2+3+…+n=
.当c=-
时,数列{an}是一个公比为-
的等比数列,即an=(-
)n-1(n∈N*).这时,数列{nan}的前n项和Sn=1+2(-
)+3(-
)2+…+n(-
)n-1①,①式两边同乘-
,得-
Sn=-
+2(-
)2+…+(n-1)(-
)n-1+n(-
)n②,①式减去②式,得(1+
)Sn=1+(-
)+(-
)+(-
)2+…+(-
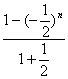)n-1-n(-
)n=
-n(-
)n.
所以Sn=
［4-(-1)n
］(n∈N*).
练习册系列答案
新思维寒假作业系列答案
相关题目
，
(n=3,4,…).