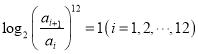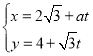题目内容
【题目】已知正方体的棱长为2,平面![]() 过正方体的一个顶点,且与正方体每条棱所在直线所成的角相等,则该正方体在平面
过正方体的一个顶点,且与正方体每条棱所在直线所成的角相等,则该正方体在平面![]() 内的正投影面积是__________.
内的正投影面积是__________.
【答案】![]()
【解析】
根据正方体的性质,结合线面角的定义,判断出平面![]() 的位置情况,最后根据正投影的定义、菱形的面积公式进行求解即可.
的位置情况,最后根据正投影的定义、菱形的面积公式进行求解即可.
正方体中所有的棱是三组平行的棱,如图所示:
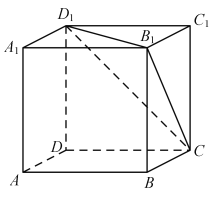
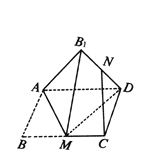
图中的正三角形![]() 所在的平面或者与该平面平行的平面为平面
所在的平面或者与该平面平行的平面为平面![]() ,满足与正方体每条棱所在直线所成的角相等,
,满足与正方体每条棱所在直线所成的角相等,
正三角形![]() 是平面
是平面![]() 截正方体所形成三角形截面中,截面面积最大者,正方体的棱长为2,
截正方体所形成三角形截面中,截面面积最大者,正方体的棱长为2,
所以正三角形![]() 的边长为:
的边长为:![]() ,正方体
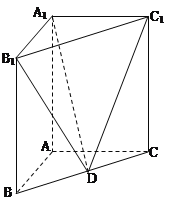
,正方体![]() 中,
中,
三个面在平面![]() 的内的正投影是三个全等的菱形,如下图所示:
的内的正投影是三个全等的菱形,如下图所示:

可以看成两个边长为![]() 的等边三角形,
的等边三角形,
所以正方体在平面![]() 内的正投影面积是:
内的正投影面积是:
![]() .
.
故答案为;![]()

练习册系列答案
相关题目