题目内容
(1)已知π<α<2π,cos(α-7π)=求sin(3π+α)与tan(α-![]() )的值;
)的值;
(2)已知2+sinAcosA=5cos2A,求tanA的值;
(3)已知sinα+cosα=![]() ,且α∈(0,π),求sin3α-cos3α的值.
,且α∈(0,π),求sin3α-cos3α的值.
解:(1)∵cos(α-7π)=-cosα=![]() ,
,
∴cosα=![]() .又π<α<2π,
.又π<α<2π,
∴![]() <α<2π,sinα=-
<α<2π,sinα=-![]() ,
,
sin(3π+α)=-sinα=![]() ,tan(α-
,tan(α-![]() )=
)=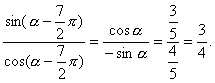
(2)将已知式化为2sin2A+2cos2A+sinA·cosA=5cos2A,
∵cosA≠0,
∴2tan2A+tanA-3=0,tanA=1或tanA=-![]() .
.
(3)sinαcosα=![]() =
=![]() ,
,
∵α∈(0,π),
∴sinα>0,cosα<0,
∴sinα-cosα>0,
∴sinα-cosα=![]() ,
,
∴sin3α-cos3α=![]() ×(1
×(1![]() )=
)=![]() .
.
思想方法小结:形如asinα+bcosα和asin2α+bsinαcosα+ccos2α的式子分别称为关于sinα、cosα的一次齐次式和二次齐次式,对涉及它们的三角式的变换常有如上的整体代入方法可供使用.

练习册系列答案
相关题目