题目内容
已知椭圆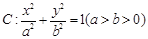 的离心率为
的离心率为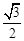 ,且经过点
,且经过点 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)如果过点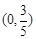 的直线与椭圆交于
的直线与椭圆交于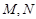 两点(
两点(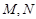 点与
点与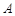 点不重合),
点不重合),
①求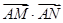 的值;
的值;
②当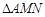 为等腰直角三角形时,求直线
为等腰直角三角形时,求直线 的方程.
的方程.
【答案】
(Ⅰ)椭圆的方程为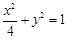 ;(Ⅱ) ①
;(Ⅱ) ①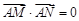 ;②直线
;②直线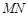 的方程为
的方程为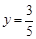 或
或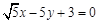 或
或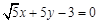 .
.
【解析】
试题分析:(Ⅰ)由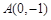 与离心率为
与离心率为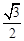 ,可求出方程;(Ⅱ) ①要求
,可求出方程;(Ⅱ) ①要求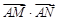 的值,可设直线
的值,可设直线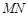 的方程,采用设而不求的方法求得;②由①知:
的方程,采用设而不求的方法求得;②由①知: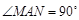 ,如果
,如果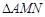 为等腰直角三角形,设
为等腰直角三角形,设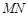 的中点为
的中点为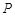 ,则
,则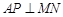 ,利用
,利用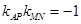 可求出
可求出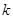 的值,从而求出直线
的值,从而求出直线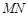 的方程为.
的方程为.
试题解析:(Ⅰ)因为椭圆经过点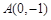 ,
,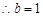 ,因为
,因为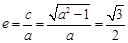 ,解得
,解得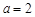 ,
,
所以椭圆的方程为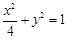 .
.
(Ⅱ) ①若过点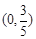 的直线的斜率不存在,此时
的直线的斜率不存在,此时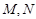 两点中有一个点与
两点中有一个点与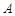 点重合,不满足题目条件.
点重合,不满足题目条件.
所以直线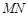 的斜率存在,设其斜率为
的斜率存在,设其斜率为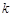 ,则
,则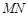 的方程为
的方程为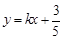 ,把
,把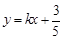 代入椭圆方程得
代入椭圆方程得 ,设
,设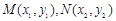 ,则
,则 ,
,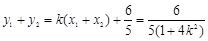 ,
,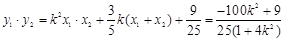 ,
,
因为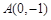 ,所以
,所以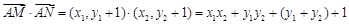
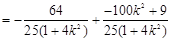
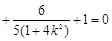 ,
,
②由①知: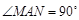 ,如果
,如果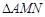 为等腰直角三角形,设
为等腰直角三角形,设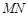 的中点为
的中点为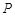 ,则
,则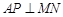 ,且
,且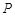
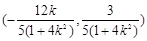 ,
,
若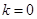 ,则
,则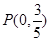 ,显然满足
,显然满足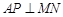 ,此时直线
,此时直线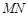 的方程为
的方程为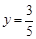 ;
;
若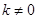 ,则
,则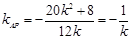 ,解得
,解得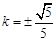 ,所以直线
,所以直线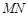 的方程为
的方程为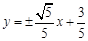 ,即
,即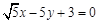 或
或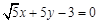 .
.
综上所述:直线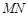 的方程为
的方程为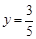 或
或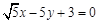 或
或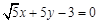 .
.
考点:1、求椭圆方程,2、直线与二次曲线的位置关系.

练习册系列答案
相关题目
已知椭圆的离心率为e,两焦点分别为F1、F2,抛物线C以F1为顶点、F2为焦点,点P为抛物线和椭圆的一个交点,若e|PF2|=|PF1|,则e的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不对 |
已知椭圆的离心率为
,焦点是(-3,0),(3,0),则椭圆方程为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在由圆O:x2+y2=1和椭圆C:
如图,在由圆O:x2+y2=1和椭圆C: 如图,A,B是椭圆C:
如图,A,B是椭圆C: