题目内容
已知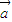
=（x，-1）与
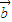=（1，
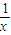），则不等式
•
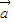≤0的解集为（ ）A．{x|x≤-1或x≥1}
B．{x|-1≤x＜0或x≥1}
C．{x|x≤-1或0≤x≤1}
D．{x|x≤-1或0＜x≤1}
【答案】分析：由
=（x，-1）与
=（1，
），结合平面向量的数量积运算公式，我们易将不等式式
•
≤0化为x-
≤0，利用分式不等式的解法，易得答案．
解答：解：∵
=（x，-1）与
=（1，
），
∴
•
=x-
故不等式
•
≤0可化为：
x-
≤0
解得：x≤-1或0＜x≤1
故不等式
•
≤0的解集为{x|x≤-1或0＜x≤1}
故选D
点评：本题考查的知识点是平面向量的数量积运算公式，及分式不等式的解法，其中分式不等式
?
是解答本题的关键，其中g（x）≠0容易被忽略．
=（x，-1）与=（1，），结合平面向量的数量积运算公式，我们易将不等式式•≤0化为x-≤0，利用分式不等式的解法，易得答案．解答：解：∵
=（x，-1）与=（1，），∴
•=x-故不等式
•≤0可化为：x-
≤0解得：x≤-1或0＜x≤1
故不等式
•≤0的解集为{x|x≤-1或0＜x≤1}故选D
点评：本题考查的知识点是平面向量的数量积运算公式，及分式不等式的解法，其中分式不等式
?是解答本题的关键，其中g（x）≠0容易被忽略． 
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知
=（x，-1）与
=（1，
），则不等式
•
≤0的解集为（ ）
| a |
| b |
| 1 |
| x |
| a |
| b |
| A、{x|x≤-1或x≥1} |
| B、{x|-1≤x＜0或x≥1} |
| C、{x|x≤-1或0≤x≤1} |
| D、{x|x≤-1或0＜x≤1} |