题目内容
已知0＜α＜π，sinα+cosα=
，求tanα的值．
| 1 |
| 5 |
∵sinα+cosα=
…①
∴平方得(sinα+cosα)2=
，即1+2sinαcosα=
可得2sinαcosα=-
因此，（sinα-cosα）2=
，得sinα-cosα=
（舍负），…②
①②联解，得sinα=
，cosα=-
∴tanα=
=-
| 1 |
| 5 |
∴平方得(sinα+cosα)2=
| 1 |
| 25 |
| 1 |
| 25 |
可得2sinαcosα=-
| 24 |
| 25 |
因此，（sinα-cosα）2=
| 49 |
| 25 |
| 7 |
| 5 |
①②联解，得sinα=
| 4 |
| 5 |
| 3 |
| 5 |
∴tanα=
| sinα |
| cosα |
| 4 |
| 3 |
练习册系列答案
名校课堂系列答案
相关题目
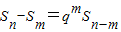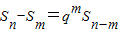恒成立．
恒成立．
恒成立．