题目内容
(1)P={x|x2-2x-3=0},S={x|ax+2=0},S?P,求a取值.
(2)A={-2≤x≤5},B={x|m+1≤x≤2m-1},B⊆A,求m取值范围.
解:(1)由x2-2x-3=0,解得x=-1,或3.∴P={-1,3}.
当a=0时,S=∅,而∅?P成立,∴a=0时成立;
当a≠0时,S={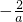 }≠∅,又S?P,∴S={-1}或{3},
}≠∅,又S?P,∴S={-1}或{3},
由此可得 或3,解得a=2,或
或3,解得a=2,或 .
.
综上可知:a可取值为0,或2,或 ..
..
(2)当m+1>2m-1,即m<2时,集合B=∅,此时满足B⊆A;
当 ,解得2≤m≤3,即2≤m≤3时,满足B⊆A.
,解得2≤m≤3,即2≤m≤3时,满足B⊆A.
综上可知:当m≤3时,满足B⊆A.
分析:(1)本题分a=0和a≠0两种情况来讨论,再据S?P即可求得a的取值范围.
(2)本题要分集合B=∅和B≠∅两种情况来讨论,再利用B⊆A,即可求得m取值范围.
点评:本题考查了集合间的关系,利用分类讨论和数形结合是解决此类问题常用的方法.
当a=0时,S=∅,而∅?P成立,∴a=0时成立;
当a≠0时,S={
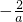 }≠∅,又S?P,∴S={-1}或{3},
}≠∅,又S?P,∴S={-1}或{3},由此可得
 或3,解得a=2,或
或3,解得a=2,或 .
.综上可知:a可取值为0,或2,或
 ..
..(2)当m+1>2m-1,即m<2时,集合B=∅,此时满足B⊆A;
当
 ,解得2≤m≤3,即2≤m≤3时,满足B⊆A.
,解得2≤m≤3,即2≤m≤3时,满足B⊆A.综上可知:当m≤3时,满足B⊆A.
分析:(1)本题分a=0和a≠0两种情况来讨论,再据S?P即可求得a的取值范围.
(2)本题要分集合B=∅和B≠∅两种情况来讨论,再利用B⊆A,即可求得m取值范围.
点评:本题考查了集合间的关系,利用分类讨论和数形结合是解决此类问题常用的方法.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
设全集U=R,集合M=
,P=
,则下列关系中正确的是( )
|
|
|
|
| A、M=P | ||
B、M
| ||
C、P
| ||
| D、M?P |