题目内容

若点P是函数y=ex-e-x-3x(-
1
2
≤x≤
1
2
)图象上任意一点，且在点P处切线的倾斜角为α，则α的最小值是（　　）
分析：对函数求导y′=ex+
1
ex
-3，由-
1
2
≤x≤
1
2
利用基本不等式可求出导数的范围，进而可求倾斜角的范围．
解答：解：y′=ex+
1
ex
-3，
∵-
1
2
≤x≤
1
2
，
∴0＞ex+
1
ex
-3≥2
ex×
1
ex
-3=-1，当且仅当x=0时取等号，
即-1≤tanα＜0
∴
3π
4
≤α＜π即倾斜角的最小值
3π
4
．
故选B．
点评：本题考查导数的几何意义：导数在切点处的值是曲线的切线斜率，以及利用基本不等式求最值，属于中档题．
练习册系列答案
相关题目
已知f(x)=2cos(ωx+θ)，(x∈R，0≤θ≤
π
2
)，g（x）=ex-x2+2ax-1，（x∈R，a为实数），y=f（x）的图象与y轴交于点(0，
3
)，且在该点处切线的斜率为-2．
（I）若点A(
π
2
，0)，点P是函数y=f（x）图象上一点，Q（x0，y0）是PA的中点，当y0=
3
2
，x0∈[
π
2
，π]时，求x0的值；
（II）当a＞1+ln2时，试问：是否存在曲线y=f（x）与y=g（x）的公切线？并证明你的结论．
已知函数，f（x）=
(x2-2ax)ex，x＞0
bx，x≤0
，g(x)=clnx+b，且x=
2
是函数y=f（x）的极值点．
（1）若方程f（x）-m=0有两个不相等的实数根，求实数m的取值范围；
（2）若直线L是函数y=f（x）的图象在点（2，f（2））处的切线，且直线L与函数Y=G（X）的图象相切于点P（x0，y0），x0∈[e-1，e]，求实数b的取值范围．
已知函数，f（x）=
(x2-2ax)ex，x＞0
bx，x≤0
，g(x)=clnx+b，且x=
2
是函数y=f（x）的极值点．
（1）若方程f（x）-m=0有两个不相等的实数根，求实数m的取值范围；
（2）若直线L是函数y=f（x）的图象在点（2，f（2））处的切线，且直线L与函数Y=G（X）的图象相切于点P（x0，y0），x0∈[e-1，e]，求实数b的取值范围．
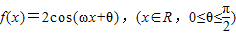已知，g（x）=ex-x2+2ax-1，（x∈R，a为实数），y=f（x）的图象与y轴交于点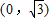，且在该点处切线的斜率为-2．
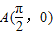（I）若点，点P是函数y=f（x）图象上一点，Q（x，y）是PA的中点，当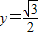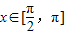，时，求x的值；
（II）当a＞1+ln2时，试问：是否存在曲线y=f（x）与y=g（x）的公切线？并证明你的结论．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网