题目内容
已知函数![]() .
.
(1)求函数![]() 的定义域;
的定义域;
(2)若函数![]() 的定义域关于坐标原点对称,试讨论它的奇偶性和单调性;
的定义域关于坐标原点对称,试讨论它的奇偶性和单调性;
(3)在(2)的条件下,记![]() 为
为![]() 的反函数,若关于
的反函数,若关于![]() 的方程
的方程![]()
有解,求![]() 的取值范围.
的取值范围.
同下
解析:
(1)![]() ,所以当
,所以当![]() 时,定义域为
时,定义域为![]() ;
;
当![]() 时,定义域为
时,定义域为![]() ;
;
当![]() 时,定义域为
时,定义域为![]() ……4分
……4分
(2)函数![]() 的定义域关于坐标原点对称,当且仅当
的定义域关于坐标原点对称,当且仅当![]() ,
,
此时,![]() . ……6分
. ……6分
对于定义域D=![]() 内任意
内任意![]() ,
,![]() ,
,
![]() ,所以
,所以![]() 为奇函数;……8分
为奇函数;……8分
当![]() ,
,![]() 在
在![]() 内单调递减;由于
内单调递减;由于![]() 为奇函数,所以在
为奇函数,所以在![]() 内单调递减; ……11分
内单调递减; ……11分
(3)![]() ,
,![]() ……14分
……14分
方程![]() 即
即![]() ,令
,令![]() ,得
,得![]() ,
,
又![]() ,所以当
,所以当![]() 时方程
时方程![]() 有解.……18分
有解.……18分
另解:令![]() ,得
,得![]() ,
,![]() ,分三种情况讨论:
,分三种情况讨论:
①方程有两根 ,解得
,解得![]()
②方程有一正一负根,![]() ,解得
,解得![]()
③方程有一正一零根,![]()
综上讨论,可知![]() .
.

练习册系列答案
相关题目
 .
. 的定义域
;
的定义域
; ,求实数
,求实数 的值.
的值. .
. 在(0,+∞)上是减函数.
在(0,+∞)上是减函数.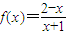 ;
; 成立,若存在求出x;若不存在,请说明理由.
成立,若存在求出x;若不存在,请说明理由. 令
令
 的定义域;
的定义域; 的奇偶性,并予以证明;
的奇偶性,并予以证明; ,猜想
,猜想 之间的关系并证明.
之间的关系并证明. ,
, 的定义域;(2)证明:
的定义域;(2)证明: ,求
,求 的取值范围。
的取值范围。