题目内容
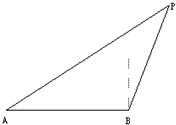 一艘海岸缉私艇巡逻至A处时发现在其正东方向20km的海面B处有一艘走私船正以vkm/h的速度向北偏东30°的方向逃窜,缉私艇以
一艘海岸缉私艇巡逻至A处时发现在其正东方向20km的海面B处有一艘走私船正以vkm/h的速度向北偏东30°的方向逃窜,缉私艇以 vkm/h的速度沿 ________的方向追击,能最快截获走私船?若v=40
vkm/h的速度沿 ________的方向追击,能最快截获走私船?若v=40 ,则追击时间至少为 ________分钟.
,则追击时间至少为 ________分钟.
北偏东60度 10
分析:先假设经过时间t到P点时恰能追上,从而可表示出∠ABP、AB、BP、AP的值,再由余弦定理可求出vt的值,进而可结合余弦定理的变形应用可求出cos∠BAP的值,从而可确定缉私艇的追击方向,再结合vt=20和v=40 ,可求出时间t的值.
,可求出时间t的值.
解答:假设经过时间t到P点时恰能追上
由题意可得∠ABP=120°,AB=20,BP=vt,AP= vt
vt
由余弦定理可得:
AP2=AB2+BP2-2AB×BPcos∠ABP
∴3v2t2=v2t2+400-2×20×vt×(- )∴vt=20或vt=-1(舍)
)∴vt=20或vt=-1(舍)
∴cos∠BAP= =
= ∴∠BAP=30°
∴∠BAP=30°
∴缉私艇应以北偏东60度追击;
当v=40 时,t=
时,t= h,即时间t=
h,即时间t= =10
=10 分钟
分钟
故答案为:北偏东60度;10
点评:本土主要考查解三角形的实际应用,考查余弦定理的应用和计算能力.

分析:先假设经过时间t到P点时恰能追上,从而可表示出∠ABP、AB、BP、AP的值,再由余弦定理可求出vt的值,进而可结合余弦定理的变形应用可求出cos∠BAP的值,从而可确定缉私艇的追击方向,再结合vt=20和v=40
 ,可求出时间t的值.
,可求出时间t的值.解答:假设经过时间t到P点时恰能追上
由题意可得∠ABP=120°,AB=20,BP=vt,AP=
 vt
vt由余弦定理可得:
AP2=AB2+BP2-2AB×BPcos∠ABP
∴3v2t2=v2t2+400-2×20×vt×(-
 )∴vt=20或vt=-1(舍)
)∴vt=20或vt=-1(舍)∴cos∠BAP=
 =
= ∴∠BAP=30°
∴∠BAP=30°∴缉私艇应以北偏东60度追击;
当v=40
 时,t=
时,t= h,即时间t=
h,即时间t= =10
=10 分钟
分钟故答案为:北偏东60度;10

点评:本土主要考查解三角形的实际应用,考查余弦定理的应用和计算能力.

练习册系列答案
相关题目
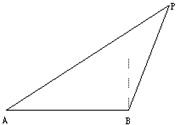 一艘海岸缉私艇巡逻至A处时发现在其正东方向20km的海面B处有一艘走私船正以vkm/h的速度向北偏东30°的方向逃窜,缉私艇以
一艘海岸缉私艇巡逻至A处时发现在其正东方向20km的海面B处有一艘走私船正以vkm/h的速度向北偏东30°的方向逃窜,缉私艇以 vkm/h的速度沿 的方向追击,能最快截获走私船?若v=40
vkm/h的速度沿 的方向追击,能最快截获走私船?若v=40 ,则追击时间至少为 分钟.
,则追击时间至少为 分钟.