Question

【题目】如图，正方形ABCD中，边长为2，E为AB中点，F是边BC上的动点．

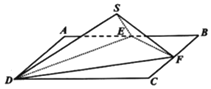
（1）将△ADE沿DE翻折90°到△SDE，求二面角S-DC-E的正切值；

（2）若，将△ADE沿DE翻折到△SDE，△BEF沿EF翻折到△SEF，接DF，设直线DS与平面DEF所成角为θ，求的最大值．

Answer 1

【答案】（1）（2）

【解析】

（1）过S作SG⊥DE于G，过G作GM⊥DC于M，连接SM，可得∠SMG为二面角S-DC-E的平面角，放入三角形中求解即可．（2）设S在面AEF上的射影为O，连接DO，则∠SDO为直线DS与面DEF所成角θ，设,利用可得SO和，换元利用函数单调性求解．

解：（1）如图，过S作SG⊥DE于G，G作GM⊥DC于M，连接SM，

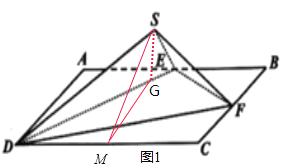
∵面SDE⊥面BCDE，面SDE∩面BCDE=DE，∴SG⊥面BCDE．

可得∠SMG为二面角S-DC-E的平面角．

在Rt△DAE中，AD=2，AE=1，∠A=90°，

∴，

∴，

∴

∴二面角S-DC-E的正切值为：．

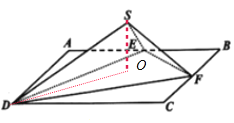
（2）设S在面AEF上的射影为O，连接DO，则∠SDO为直线DS与平面DEF所成角θ．

∴SE⊥SD，SE⊥SB，∴SE⊥面DSF．

设，则CF=2-x．

．

在△DSF中，DS=2，SF=x，．

可得

，

∵

∴．

∴，

令，t∈（0，]，

∵函数在（0，）递减，

∴当t=，即x=2时,sinθ最大，最大值为．