题目内容
已知椭圆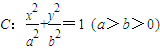 的长半轴是短半轴的
的长半轴是短半轴的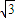 倍,直线
倍,直线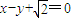 经过
经过椭圆C的一个焦点.
(1)求椭圆C的方程;
(2)设一条直线 l与椭圆C交于A、B两点,坐标原点O到直线l的距离为
 ,求△AOB面积的最大值.
,求△AOB面积的最大值.
【答案】分析:(1)根据直线 经过椭圆C的一个焦点,可求c.利用长半轴是短半轴的
经过椭圆C的一个焦点,可求c.利用长半轴是短半轴的 倍,可求椭圆C的方程;
倍,可求椭圆C的方程;
(2)分类讨论:AB⊥x轴时;AB与x轴不垂直,将直线方程代入椭圆方程,进而可求AB的长,从而可表示△AOB面积,故可求面积的最大值.
解答:解:(1) 与x轴的交点为
与x轴的交点为 ,
,
∴
又 ,c2=a2-b2=2
,c2=a2-b2=2
∴ ,b=1
,b=1
椭圆C的方程为: . (5分)
. (5分)
(2)设A(x1,y1),B(x2,y2).
①当AB⊥x轴时, ,
, 、
、
或 、
、
则: (6分)
(6分)
②当AB与x轴不垂直时,设直线AB的方程为y=kx+m.
由已知 ,得
,得 .
.
把y=kx+m代入椭圆方程,整理得(3k2+1)x2+6kmx+3m2-3=0,(8分)
△=(6km)2-12(3k2+1)(m2-1)=3(9k2+1)>0
 ,
, .
.
∴|AB|2=(1+k2)(x2-x1)2= =
= =
= . (12分)
. (12分)
当且仅当 ,即
,即 时等号成立.
时等号成立.
由①、②可知:|AB|max=2.
∴当|AB|最大时,△AOB面积取最大值 .(14分)
.(14分)
点评:本题以椭圆为载体,考查直线与椭圆的位置关系,关键是联立方程,组成方程组,进而利用根与系数的关系求解.
 经过椭圆C的一个焦点,可求c.利用长半轴是短半轴的
经过椭圆C的一个焦点,可求c.利用长半轴是短半轴的 倍,可求椭圆C的方程;
倍,可求椭圆C的方程;(2)分类讨论:AB⊥x轴时;AB与x轴不垂直,将直线方程代入椭圆方程,进而可求AB的长,从而可表示△AOB面积,故可求面积的最大值.
解答:解:(1)
 与x轴的交点为
与x轴的交点为 ,
,∴

又
 ,c2=a2-b2=2
,c2=a2-b2=2∴
 ,b=1
,b=1椭圆C的方程为:
 . (5分)
. (5分)(2)设A(x1,y1),B(x2,y2).
①当AB⊥x轴时,
 ,
, 、
、
或
 、
、
则:
 (6分)
(6分)②当AB与x轴不垂直时,设直线AB的方程为y=kx+m.
由已知
 ,得
,得 .
.把y=kx+m代入椭圆方程,整理得(3k2+1)x2+6kmx+3m2-3=0,(8分)
△=(6km)2-12(3k2+1)(m2-1)=3(9k2+1)>0
 ,
, .
.∴|AB|2=(1+k2)(x2-x1)2=
 =
= =
= . (12分)
. (12分)当且仅当
 ,即
,即 时等号成立.
时等号成立.由①、②可知:|AB|max=2.
∴当|AB|最大时,△AOB面积取最大值
 .(14分)
.(14分)点评:本题以椭圆为载体,考查直线与椭圆的位置关系,关键是联立方程,组成方程组,进而利用根与系数的关系求解.

练习册系列答案
相关题目
 百公里)的中心
百公里)的中心 为一个焦点的椭圆. 如图,已知探测器的近火星点(轨道上离火星表面最近的点)
为一个焦点的椭圆. 如图,已知探测器的近火星点(轨道上离火星表面最近的点) 到火星表面的距离为
到火星表面的距离为 百公里,远火星点(轨道上离火星表面最远的点)
百公里,远火星点(轨道上离火星表面最远的点)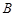 到火星表面的距离为800百公里. 假定探测器由近火星点
到火星表面的距离为800百公里. 假定探测器由近火星点 的距离为
的距离为 百公里时进行变轨,其中
百公里时进行变轨,其中 、
、 分别为椭圆的长半轴、短半轴的长,求此时探测器与火星表面的距离(精确到1百公里).
分别为椭圆的长半轴、短半轴的长,求此时探测器与火星表面的距离(精确到1百公里).
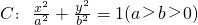 的长半轴是短半轴的
的长半轴是短半轴的 倍,直线
倍,直线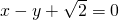 经过
经过 ,求△AOB面积的最大值.
,求△AOB面积的最大值.