题目内容
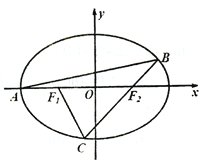
【题目】如图,已知矩形![]() 所在平面与
所在平面与![]() 所在平面互相垂直,
所在平面互相垂直,![]() ,
,![]() .
.

(1)若M为![]() 中点,N为
中点,N为![]() 中点,证明:
中点,证明:![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,且
,且![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的大小.
的大小.
【答案】(1)证明见解析;(2)15°.
【解析】
(1)取![]() 的中点
的中点![]() ,证明四边形
,证明四边形![]() 是平行四边形得出
是平行四边形得出![]() ,故而结论得证;
,故而结论得证;
(2)在平面![]() 上构造矩形
上构造矩形![]() ,使得
,使得![]() 在矩形边
在矩形边![]() 上,根据
上,根据![]() 与平面
与平面![]() 所成角的大小计算
所成角的大小计算![]() ,再利用勾股定理或圆的性质计算
,再利用勾股定理或圆的性质计算![]() .
.
(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
(2)解:在平面![]() 上作矩形
上作矩形![]() ,使得
,使得![]() 在边
在边![]() 上,
上,
过![]() 作
作![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,
,
则![]() ,
,![]() ,又
,又![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
又![]() ,故
,故![]() ,
,
又![]() ,
,![]() ,
,
![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() .
.
![]() 为
为![]() 与平面
与平面![]() 所成的角,即
所成的角,即![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
设![]() ,则
,则![]() ,于是
,于是![]() ,
,![]() ,
,
![]() ,
,![]() ,解得
,解得![]() ,
,
又![]() ,故
,故![]() ,
,![]() ,
,
![]() ,
,
![]() .
.


 名校课堂系列答案
名校课堂系列答案【题目】某校在高一部分学生中调查男女同学对某项体育运动的喜好情况,其二维条形图如图(黑色代表喜好,白色代表不喜好).
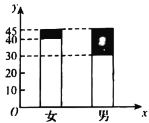
(1)写出![]() 列联表;
列联表;
(2)能否有99%的把握认为喜好这项体育运动与性别有关;
(3)在这次调查中从喜好这项体育活动的一名男生和两名女生中任选两人进行专业培训,求恰是一男一女的概率.
附: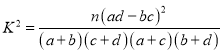
| 0.25 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.83 |
【题目】某客户准备在家中安装一套净水系统,该系统为三级过滤,使用寿命为十年.如图所示,两个一级过滤器采用并联安装,二级过滤器与三级过滤器为串联安装。

其中每一级过滤都由核心部件滤芯来实现。在使用过程中,一级滤芯和二级滤芯都需要不定期更换(每个滤芯是否需要更换相互独立),三级滤芯无需更换,若客户在安装净水系统的同时购买滤芯,则一级滤芯每个![]() 元,二级滤芯每个
元,二级滤芯每个![]() 元.若客户在使用过程中单独购买滤芯,则一级滤芯每个
元.若客户在使用过程中单独购买滤芯,则一级滤芯每个![]() 元,二级滤芯每个
元,二级滤芯每个![]() 元。现需决策安装净水系统的同时购滤芯的数量,为此参考了根据
元。现需决策安装净水系统的同时购滤芯的数量,为此参考了根据![]() 套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表,其中图是根据
套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表,其中图是根据![]() 个一级过滤器更换的滤芯个数制成的柱状图,表是根据
个一级过滤器更换的滤芯个数制成的柱状图,表是根据![]() 个二级过滤器更换的滤芯个数制成的频数分布表.
个二级过滤器更换的滤芯个数制成的频数分布表.

二级滤芯更换频数分布表
二级滤芯更换的个数 |
|
|
频数 |
|
|
以![]() 个一级过滤器更换滤芯的频率代替
个一级过滤器更换滤芯的频率代替![]() 个一级过滤器更换滤芯发生的概率,以
个一级过滤器更换滤芯发生的概率,以![]() 个二级过滤器更换滤芯的频率代替
个二级过滤器更换滤芯的频率代替![]() 个二级过滤器更换滤芯发生的概率.
个二级过滤器更换滤芯发生的概率.
(1)求一套净水系统在使用期内需要更换的各级滤芯总个数恰好为![]() 的概率;
的概率;
(2)记![]() 表示该客户的净水系统在使用期内需要更换的一级滤芯总数,求
表示该客户的净水系统在使用期内需要更换的一级滤芯总数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)记![]() ,
,![]() 分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若
分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若![]() ,且
,且![]() ,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定
,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定![]() ,
,![]() 的值.
的值.