题目内容
已知PA⊥面AC，且PA=AD，M为AB中点，ABCD为矩形，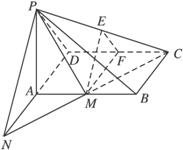
（1）求证：面PMC⊥面PCD；
（2）分别记面PCB、面PMC与面PAD所成角为α、β，求证：
为定值.
证明：(1)MP=
,
MC=,PA=AD=BC,
BM=AM,∴MP=MC.取PC中点E,则
ME⊥PC.取CD中点F,则MF⊥CD.CD⊥AD,∴CD⊥PD,CD⊥EF
CD⊥面MEF1,∴CD⊥ME.∴ME⊥面PCD.故面PMC⊥面PCD.
(2)α=∠APB.β=∠CPD.
∴tanα=
,tanβ=
.
∴tanαtanβ=
·
=
=
为定值.
练习册系列答案
相关题目
如图，已知PA⊥⊙O所在的平面，AB是⊙O的直径，AB=2，C是⊙O上一点，且AC=BC，PC与⊙O所在的平面成45°角，E是PC中点．F为PB中点．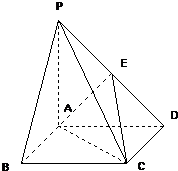
已知：如图，在四棱锥P-ABCD中，四边形ABCD为正方形，PA⊥面ABCD，且PA=AB=2，E为PD中点．
如图，已知PA⊥⊙O所在的平面，AB是⊙O的直径，AB=2，C是⊙O上一点，且AC=BC，PC与⊙O所在的平面成45°角，E是PC中点，F为PB中点．