Question

如图，在直三棱柱ABC—A₁B₁C₁中，底面是等腰直角三角形，∠ACB=90°，侧棱AA₁=2，D、E分别是CC₁与A₁B的中点，点E在平面ABD上的射影是△ABD的重心G.

(1)求A₁B与平面ABD所成角的余弦值；

(2)求点A₁到平面AED的距离.

Answer 1

解析：(1)连结，则是在面ABD的射影，即∠A₁BG是A₁B与平面ABD所成的角.

如图所示建立坐标系，坐标原点为O.设=2a,则A(2a,0,0),B(0,2a,0),D(0,0,1),?A₁(2a,0,2),E(a,a,1),G(,,).

∴=(,,),=(0,-2a,1).?

∴·=-a²+=0，解得a=1.

∴=(2,-2,2),=(,-,).?

∴cos∠A₁BG===.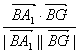

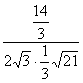(2)由(1)有A(2,0,0),A₁(2,0,2),E(1,1,1),D(0,0,1)，

·=(-1,1,1)·(-1,-1,0)=0,?

·=(0,0,2)·(-1,-1,0)=0.

∴ED⊥平面AA₁E.又ED平面AED,

∴平面AED⊥平面AA₁E.

又面AED∩面AA₁E=AE，

∴点A₁在平面AED的射影K在上.

设=λ,则=+=(-λ,λ,λ-2).

由·=0,即λ+λ+λ-2=0,解得λ=.

∴=(-,,-).

∴||=.

故A₁到平面AED的距离为.