题目内容
已知函数f(x)=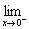
在区间(-∞,+∞)是增函数，则常数a的取值范围是( ) A．1≤a≤2 B．a≤1或a≥2
C．1＜a＜2 D．a＜1或a＞2
A
解析：本题考查对函数单调性的理解以及求函数极限运算.因为函数f(x)在[0，+∞]是增函数，在(-∞，0)也是增函数，故要使函数f(x)在(-∞，+∞)是增函数只需 (x3+a2-3a+2)≤0且a2-3a+2≤0，解之得1≤a≤2.
练习册系列答案
相关题目
已知函数f(x)=
在（0，+∞）上单调递增，则实数k的取值范围是（ ）
| -k |
| x |
| A、（-∞，0） |
| B、（0，+∞） |
| C、（1，+∞） |
| D、（-∞，1） |
已知函数f(x)=
在区间[1，2]上的最大值为A，最小值为B，则A-B=（ ）
| 1 |
| x |
A、
| ||
B、-
| ||
| C、1 | ||
| D、-1 |
在x＝0，x＝
处存在极值。
]上单调递增，则正实数