题目内容
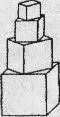
一单位正方体形积木,平放在桌面上,在其上放置5个小正方体形积木摆成塔形,其中上面正方体中下底的四个顶点是下面相邻正方体中上底面各边的中点,则6个正方体暴露在外面部分的面积和为
.
| 71 |
| 8 |
| 71 |
| 8 |
分析:由已知中一单位正方体形积木,平放在桌面上,在其上放置5个小正方体形积木摆成塔形,其中上面正方体中下底的四个顶点是下面相邻正方体中上底面各边的中点,我们易得相邻两个正方体中,上边一个正方体的侧面积为下边一个正方体的侧面积的一半,进而得到各个正方体的侧面积组成一个以4首项,以
为公比的等比数列,由此求出各侧面的和,加上顶面暴露在外面部分的面积和为1,累加后即可得到答案.
| 1 |
| 2 |
解答:解:最下边正方体的侧面积为4×1=4
从下边数第二个正方体的侧面积为4×
=2
从下边数第三个正方体的侧面积为4×
=1
…
即相邻两个正方体中,上边一个正方体的侧面积为下边一个正方体的侧面积的一半.
各个正方体的侧面积组成一个以4首项,以
为公比的等比数列
故Sn=
当n=6时
S6=
=
而除侧面外其它面的和为1,
故6个正方体暴露在外面部分的面积和为
+1=
故答案为:
从下边数第二个正方体的侧面积为4×
| 1 |
| 2 |
从下边数第三个正方体的侧面积为4×
| 1 |
| 4 |
…
即相邻两个正方体中,上边一个正方体的侧面积为下边一个正方体的侧面积的一半.
各个正方体的侧面积组成一个以4首项,以
| 1 |
| 2 |
故Sn=
4[1-(
| ||
1-
|
当n=6时
S6=
4[1-(
| ||
1-
|
| 63 |
| 8 |
而除侧面外其它面的和为1,
故6个正方体暴露在外面部分的面积和为
| 63 |
| 8 |
| 71 |
| 8 |
故答案为:
| 71 |
| 8 |
点评:本题考查的知识点是棱柱的结构特征,等比数列的前n项和,其中根据已知条件将问题转化为等比数列的前n项和问题,是解答本题的关键.解答时易忽略6个正方体暴露在外面部分不包括下底面,但包括上底面,而错解为
或
.
| 63 |
| 8 |
| 79 |
| 8 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,一单位正方体形积木,平放于桌面上,并且在其上方放置若干个小正方体形积木摆成塔形,其中上面正方体中下底面的四个顶点是下面相邻正方体中上底面各边的中点,如果所有正方体暴露在外面部分的面积之和超过8.8,则正方体的个数至少是( )
如图,一单位正方体形积木,平放于桌面上,并且在其上方放置若干个小正方体形积木摆成塔形,其中上面正方体中下底面的四个顶点是下面相邻正方体中上底面各边的中点,如果所有正方体暴露在外面部分的面积之和超过8.8,则正方体的个数至少是( )