题目内容
若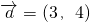 ,
,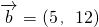 ,则
,则 与
与 夹角的余弦值为________.
夹角的余弦值为________.

分析:先利用两个向量的数量积的定义求出
 =|
=| |•|
|•| |cosθ=65cosθ.再利用两个向量的数量积公式求得
|cosθ=65cosθ.再利用两个向量的数量积公式求得 =63,
=63,由65cosθ=63,求出cosθ 的值即为所求.
解答:若
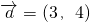 ,
,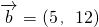 ,则|
,则| |=5,|
|=5,| |=13.
|=13.设
 与
与 夹角为θ,∴
夹角为θ,∴ =|
=| |•|
|•| |cosθ=65cosθ.
|cosθ=65cosθ.又
 =(3,4)•(5,12)=15+48=63,
=(3,4)•(5,12)=15+48=63,故 65cosθ=63,∴cosθ=
 .
.故答案为
 .
.点评:本题主要考查两个向量的数量积的定义,数量积公式的应用,求出
 =65cosθ,是解题的关键,属于基础题.
=65cosθ,是解题的关键,属于基础题. 
练习册系列答案
相关题目
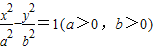 ,A,C分别是双曲线虚轴的上、下端点,B,F分别是双曲线的左顶点和左焦点.若双曲线的离心率为2,则
,A,C分别是双曲线虚轴的上、下端点,B,F分别是双曲线的左顶点和左焦点.若双曲线的离心率为2,则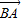 与
与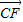 夹角的余弦值为 .
夹角的余弦值为 .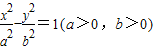 ,A,C分别是双曲线虚轴的上、下端点,B,F分别是双曲线的左顶点和左焦点.若双曲线的离心率为2,则
,A,C分别是双曲线虚轴的上、下端点,B,F分别是双曲线的左顶点和左焦点.若双曲线的离心率为2,则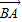 与
与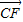 夹角的余弦值为 .
夹角的余弦值为 . ,
, ,则
,则 与
与 夹角的余弦值为 .
夹角的余弦值为 .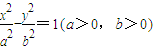 ,A,C分别是双曲线虚轴的上、下端点,B,F分别是双曲线的左顶点和左焦点.若双曲线的离心率为2,则
,A,C分别是双曲线虚轴的上、下端点,B,F分别是双曲线的左顶点和左焦点.若双曲线的离心率为2,则 与
与 夹角的余弦值为 .
夹角的余弦值为 .