题目内容
在平面直角坐标系中,点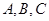 的坐标分别为
的坐标分别为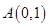 、
、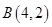 、
、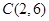 ,如果
,如果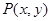
是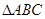 围成的区域(含边界)上的点,那么
围成的区域(含边界)上的点,那么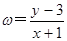 的范围是 .
的范围是 .
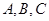 的坐标分别为
的坐标分别为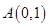 、
、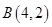 、
、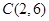 ,如果
,如果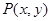
是
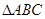 围成的区域(含边界)上的点,那么
围成的区域(含边界)上的点,那么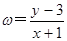 的范围是 .
的范围是 .
试题分析:
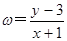 可以看成是可行域内的点与定点
可以看成是可行域内的点与定点 的连线的斜率,画出三角形,可知点
的连线的斜率,画出三角形,可知点 在
在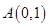 处时,
处时, 的斜率最小为-2;点
的斜率最小为-2;点 在
在 处时,
处时, 的斜率最大为1,所以取值范围是
的斜率最大为1,所以取值范围是 .考点:
.考点:点评:求目标函数的最值,必须先准确地作出线性约束条件表示的可行域,再根据目标函数的几何意义确定取得最优解的点,进而求出目标函数的最值.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 是由直线
是由直线 和
和 所围成的三角形(含边界与内部).若点
所围成的三角形(含边界与内部).若点 ,则目标函数
,则目标函数 的最大值为( )
的最大值为( )



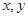 满足线性约束条件
满足线性约束条件
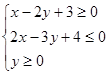 ,若目标函数
,若目标函数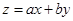 (其中
(其中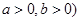 的最大值为3,则
的最大值为3,则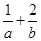 的最小值为
的最小值为 。
。 的取大值是______________.
的取大值是______________. 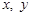 满足
满足 ,则
,则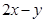 的最小值为 .
的最小值为 . 满足不等式组
满足不等式组 ,那么目标函数
,那么目标函数 的最小值是______.
的最小值是______.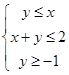 下,过点
下,过点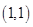 目标函数
目标函数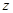 取得最大值10,则目标函数
取得最大值10,则目标函数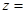 ______(写出一个适合题意的目标函数即可);
______(写出一个适合题意的目标函数即可);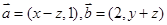 ,且
,且 ,若变量x,y满足约束条件
,若变量x,y满足约束条件 则z的最大值为
则z的最大值为