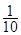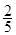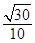题目内容
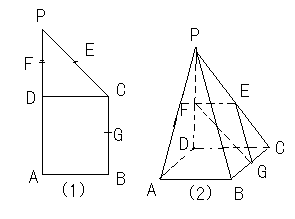
((本小题满分14分)如图,四棱锥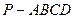 的底面
的底面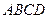 是正方形,侧棱
是正方形,侧棱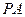
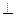 底面
底面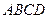 ,
,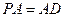 ,
,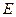 、
、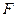 分别是棱
分别是棱 、
、 的中点.
的中点.
(1)求证: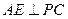 ; (2) 求直线
; (2) 求直线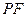 与平面
与平面 所成的角的正切值
所成的角的正切值
(方法一)解:因为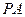
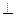 底
底 面
面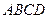 ,所以
,所以 [
[
因为底面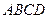 是正方形,所以
是正方形,所以

 ,故
,故
 ,所以
,所以
 , (3分)
, (3分)
又因为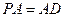 ,点
,点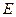 是棱
是棱 的中点,
的中点,
所以 ,
, ,故
,故
 ,所以
,所以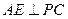 . (7分)
. (7分)
(2)过点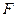 作
作 ,连接
,连接
由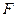 是棱
是棱 的中点,底面是正方形可得
的中点,底面是正方形可得 ,又由
,又由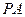
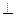 底面
底面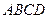 得到
得到 ,
, ,
, ,所以
,所以 为直线
为直线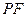 与平面
与平面 所成的角, (10分)
所成的角, (10分)
设 ,得到
,得到 ,
,
在 中,
中,  ,
, . (14分)
. (14分)
(方法二)解:以A为原点,分别以 的方向为
的方向为 轴正方向建立空间直角坐标系,设
轴正方向建立空间直角坐标系,设 [来源:学科网ZXXK]
[来源:学科网ZXXK]
则 , (2分)
, (2分)
∵点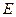 、
、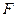 分别是棱
分别是棱 、
、 的中点,
的中点,
∴  ,
, .
. ,
, (4分)
(4分) ,所以
,所以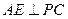 . (6分)
. (6分)
(2)又由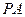
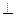 底面
底面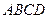 得到
得到 ,
, ,
, ,
,
取 的法向量
的法向量 =(-1,1,0), (10分)
=(-1,1,0), (10分)
设直线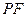 与平面
与平面 所成的角
所成的角
解析

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
已知向量a=(1,1,0),b=(-1,0,2),且ka+b与2a-b互相垂直,则k值是( )
| A.1 | B.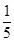 | C.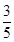 | D.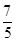 |
如图,正四面体 的顶点
的顶点 分别在两两垂直的三条射线
分别在两两垂直的三条射线 上,则在下列命题中,错误的为( )
上,则在下列命题中,错误的为( )
A. 是正三棱锥 是正三棱锥 |
B.直线 平面 平面 |
C.直线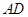 与 与 所成的角是 所成的角是 |
D.二面角 为 为 |
已知平面α内有一个点A(2,-1,2),α的一个法向量为n=(3,1,2),则下列点P中,在平面α内的是( )
| A.(1,-1,1) | B.(1,3,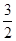 ) ) |
C.(1,-3,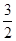 ) ) | D.(-1,3,-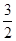 ) ) |
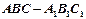 的三视图如图所示,
的三视图如图所示, 其中正视图
其中正视图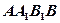 和侧视图
和侧视图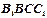 均为矩形,俯视图
均为矩形,俯视图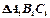 中,
中,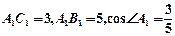 。
。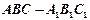 中,求证:
中,求证: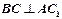 ;
;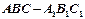 中,若
中,若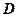 是底边
是底边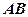 的中点,求证:
的中点,求证: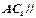 平面
平面 ;
;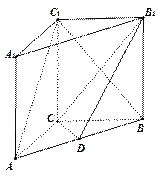
 本小题满分12分)如图,在三棱柱
本小题满分12分)如图,在三棱柱 中,
中,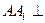 面
面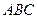 ,
,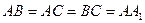 ,
,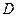 ,
,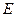 分别为
分别为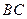 ,
,
 的中点.
的中点.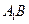 ∥平面
∥平面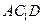 ; (2)求证:
; (2)求证: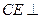 平面
平面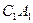 与平面
与平面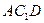 所成的角的
所成的角的 正弦值.
正弦值.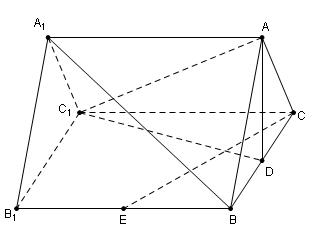
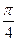 。
。