题目内容
15.已知实数x,y满足$\left\{\begin{array}{l}{x≥1}\\{x-2y+1≤0}\\{x+y-4≤0}\end{array}\right.$,此不等式组表示的平面区域的面积为$\frac{4}{3}$,目标函数Z=2x-y的最小值为-1.分析 由题意作出其平面区域,求出三个点的坐标,从而求三角形的面积,再结合函数图象求目标函数Z=2x-y的最小值.
解答 解:由题意作出其平面区域,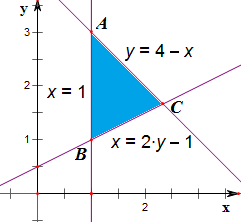
x=1,y=4-x,x=2y-1两两联立解得,
A(1,3),B(1,1),C($\frac{7}{3}$,$\frac{5}{3}$);
故S△ABC=$\frac{1}{2}$×2×($\frac{7}{3}$-1)=$\frac{4}{3}$;
当x取最小值,y取最大值,即过点A(1,3)时,
目标函数Z=2x-y有最小值2-3=-1;
故答案为:$\frac{4}{3}$;-1.
点评 本题考查了简单线性规划,作图要细致认真,同时考查了直线交点的求法及三角形的面积公式应用,属于中档题.

练习册系列答案
相关题目
5.已知点A是半径为1的⊙O外一点,且AO=2,若M,N是⊙O一条直径的两个端点,则$\overrightarrow{AM}$$•\overrightarrow{AN}$=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3.定义在R上的奇函数f(x)和定义在{x|x≠0}上的偶函数g(x)分别满足f(x)=$\left\{\begin{array}{l}{{2}^{x}-1(0≤x<1)}\\{\frac{1}{x}(x≥1)}\end{array}\right.$,g(x)=log2x(x>0),若存在实数a,使得f(a)=g(b)成立,则实数b的取值范围是( )
| A. | [-2,2] | B. | [-$\frac{1}{2}$,0)∪(0,$\frac{1}{2}$] | C. | [-2,-$\frac{1}{2}$]∪[$\frac{1}{2}$,2] | D. | (-∞,-2]∪[2,+∞) |
10.设P,Q分别为直线x-y=0和圆x2+(y-6)2=2上的点,则|PQ|的最小值为( )
| A. | $2\sqrt{2}$ | B. | $3\sqrt{2}$ | C. | $4\sqrt{2}$ | D. | 4 |
20.某高中校共有学生1000名,各年级男女学生人数如下表,已知在全校学生中随机抽取1名,抽到高二男生的概率是0.16.
现用分层抽样的方法,在全校抽取40名学生,则应在高三年级抽取的学生人数为15.
| 高一年级 | 高二年级 | 高三年级 | |
| 女生 | 162 | 140 | Y |
| 男生 | 163 | X | 184 |
4.设A={x|y=$\sqrt{2x-1}$,x∈R},B={x|x2-3x-18<0},则A∩B=( )
| A. | ($\frac{1}{2}$,6) | B. | ($\frac{1}{2}$,3) | C. | [$\frac{1}{2}$,6) | D. | [$\frac{1}{2}$,3) |
5.函数f(x)=ln(x2-2x-3)的单调递减区间为( )
| A. | (-∞,1) | B. | (1,+∞) | C. | (-∞,-1) | D. | (3,+∞) |