题目内容
已知c>0.设命题P:![]() cn=0.
cn=0.
命题Q:当x∈[![]() ,2]时,函数f(x)=x+
,2]时,函数f(x)=x+![]() >
>![]() 恒成立.
恒成立.
如果P或Q为真命题,P且Q为假命题,求c的取值范围.
分析:由![]() cn=0得,0<c<1.∴P:0<c<1,
cn=0得,0<c<1.∴P:0<c<1,
由x∈[![]() ,2]时,函数f(x)=x+
,2]时,函数f(x)=x+![]() >
>![]() 恒成立,想到
恒成立,想到![]() <f(x)min,故需求f(x)在[
<f(x)min,故需求f(x)在[![]() ,2]上的最小值.
,2]上的最小值.
解析:∵![]() cn=0且c>0,∴0<c<1,∴P:0<c<1.
cn=0且c>0,∴0<c<1,∴P:0<c<1.
x∈[![]() ,2]时,x+
,2]时,x+![]() ≥2当且仅当x=1时“=”成立.
≥2当且仅当x=1时“=”成立.
∵x∈[![]() ,2]时,函数f(x)=x+
,2]时,函数f(x)=x+![]() >
>![]() 恒成立,∴
恒成立,∴![]() <2.∴c>
<2.∴c>![]() .
.
Q:c>![]() ,
,
如果P或Q为真命题,则c>0;
如果P且Q为假命题,则0<c≤![]() 或c≥1.
或c≥1.
综上得0<c≤![]() 或c≥1.
或c≥1.

练习册系列答案
相关题目
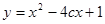 在
在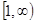 上恒为增函数.若P或Q为真, P且Q为假,求c的取值范围。
上恒为增函数.若P或Q为真, P且Q为假,求c的取值范围。 在实数集R上为增函数,命题q:不等式
在实数集R上为增函数,命题q:不等式 在R上恒成立.若命题p或q是真命题, p且q是假命题,求c的取值范围.
在R上恒成立.若命题p或q是真命题, p且q是假命题,求c的取值范围.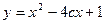 在
在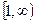 上恒为增函数.若P或Q为真,P且Q为假,求c的取值范围。
上恒为增函数.若P或Q为真,P且Q为假,求c的取值范围。