题目内容
某商家推出一款简单电子游戏,弹射一次可以将三个相同的小球随机弹到一个正六边形的顶点与中心共七个点中的三个位置上(如图),用S表示这三个球为顶点的三角形的面积.规定:当三球共线时,S=0;当S最大时,中一等奖,当S最小时,中二等奖,其余情况不中奖,一次游戏只能弹射一次.
(1)求甲一次游戏中能中奖的概率;
(2)设这个正六边形的面积是6,求一次游戏中随机变量S的分布列及期望值.
(1)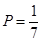 ;(2)S的可能值为:0,1,2,3,其分布列为
;(2)S的可能值为:0,1,2,3,其分布列为S 0 1 2 3 P 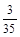
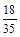
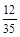
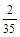
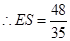 .
.
解析试题分析:(1)由题意可知,这是随机变量的等可能事件的概率问题,弹射一次可以将三个相同的小球随机弹到一个正六边形的顶点与中心共七个点中的三个位置上共有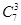 种方法,当S最大时它的方法数有
种方法,当S最大时它的方法数有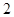 种,当S最小时,即
种,当S最小时,即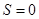 共有
共有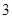 种方法,一次游戏中能中奖的方法数有
种方法,一次游戏中能中奖的方法数有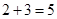 种,由古典概率求法可得甲一次游戏中能中奖的概率;(2)设这个正六边形的面积是6,一次游戏中随机变量S的可能值为:0,1,2,3,分别求出它们的概率,得分布列,进而可求得期望值.
种,由古典概率求法可得甲一次游戏中能中奖的概率;(2)设这个正六边形的面积是6,一次游戏中随机变量S的可能值为:0,1,2,3,分别求出它们的概率,得分布列,进而可求得期望值.
试题解析:(1)甲中奖的概率为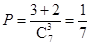
(2)S的可能值为:0,1,2,3,其分布列为S 0 1 2 3 P 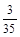
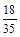
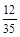
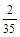
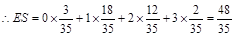
考点:古典概率,分布列及期望值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某公司研制出一种新型药品,为测试该药品的有效性,公司选定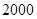 个药品样本分成三组,测试结果如下表:
个药品样本分成三组,测试结果如下表:
| 分组 | 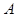 组 组 | 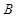 组 组 |  组 组 |
| 药品有效 | 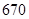 | 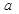 | 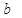 |
| 药品无效 | 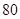 | 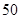 | 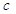 |
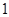 个,抽到
个,抽到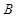 组药品有效的概率是
组药品有效的概率是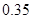 .
.(1)现用分层抽样的方法在全体样本中抽取
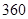 个测试结果,问应在
个测试结果,问应在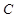 组抽取样本多少个? [来源:学优]
组抽取样本多少个? [来源:学优](2)已知
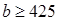 ,
,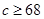 ,求该药品通过测试的概率(说明:若药品有效的概率不小于
,求该药品通过测试的概率(说明:若药品有效的概率不小于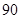 %,则认为测试通过).
%,则认为测试通过). 在一次抢险救灾中,某救援队的50名队员被分别分派到四个不同的区域参加救援工作,其分布的情况如下表,从这50名队员中随机抽出2人去完成一项特殊任务.
| 区域 | A | B | C | D |
| 人数 | 20 | 10 | 5 | 15 |
(2)若这2人来自区域A,D,并记来自区域A队员中的人数为X,求随机变量X的分布列及数学期望.
 ,服用B有效的概率为
,服用B有效的概率为 .
.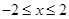 ,
,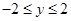 ,点
,点 的坐标为
的坐标为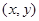 .
.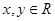 时,点
时,点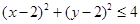 的概率;
的概率;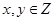 时,点
时,点 表示.
表示.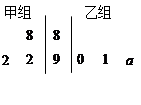
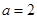 时,分别从甲、乙两组中各随机选取一名同学,记这两名同学数学成绩之差的绝对值为
时,分别从甲、乙两组中各随机选取一名同学,记这两名同学数学成绩之差的绝对值为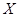 ,求随机变量
,求随机变量 的等差数列,他第一次测试合格的概率不超过
的等差数列,他第一次测试合格的概率不超过 ,且他直到第二次测试才合格的概率为
,且他直到第二次测试才合格的概率为 。
。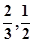 且每棵树是否存活互不影响,求移栽的5棵树中:
且每棵树是否存活互不影响,求移栽的5棵树中: 的分布列与期望.
的分布列与期望.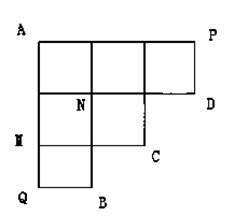
 ;
;