��Ŀ����
����Ŀ���Ķ�������ϣ��������̽������y=x2�� ![]() ��ͼ��д��ͼ����������������õ��Ľ��ۣ����Բ²�����������Ӧ��ͼ�� �Ķ����ϣ�
��ͼ��д��ͼ����������������õ��Ľ��ۣ����Բ²�����������Ӧ��ͼ�� �Ķ����ϣ�
�ҹ�������ѧ�һ���������˵����ȱ��ʱ��ֱ�ۣ�������ʱ���������ν�ϰٰ�ã����ѷּ������ݣ�
����ѧ��ѧϰ���о��У����ú�����ͼ�����о����������ʣ�Ҳ���ú����Ľ���ʽ����ĥ������ͼ�����������������һ��Ӧ�ú����������о���Ӧͼ����״�����ӣ�
���ں���y= ![]() �����ǿ���ͨ������ʽ���о�����ͼ������ʣ��磺
�����ǿ���ͨ������ʽ���о�����ͼ������ʣ��磺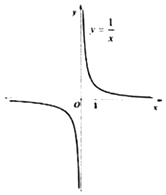
��1���ں���y= ![]() �У���x��0�������Ʋ������Ӧ��ͼ����y�ᣬ��ͼ����y��ཻ����y��0�������Ʋ������Ӧ��ͼ����x�ᣬ��ͼ����x��ཻ��
�У���x��0�������Ʋ������Ӧ��ͼ����y�ᣬ��ͼ����y��ཻ����y��0�������Ʋ������Ӧ��ͼ����x�ᣬ��ͼ����x��ཻ��
��2���ں���y= ![]() �У���x��0ʱy��0����x��0ʱy��0�������Ʋ������Ӧ��ͼ��ֻ���ڵ�һ�������ޣ�
�У���x��0ʱy��0����x��0ʱy��0�������Ʋ������Ӧ��ͼ��ֻ���ڵ�һ�������ޣ�
��3���ں���y= ![]() �У���x�ʣ�0��+�ޣ���y��0���ҵ�x������ʱy��С�������Ʋ������Ӧ��ͼ��Խ����Խ����x���x�ʣ����ޣ�0������y��0���ҵ�x��Сʱy���������Ʋ������Ӧ��ͼ��Խ����Խ����x�
�У���x�ʣ�0��+�ޣ���y��0���ҵ�x������ʱy��С�������Ʋ������Ӧ��ͼ��Խ����Խ����x���x�ʣ����ޣ�0������y��0���ҵ�x��Сʱy���������Ʋ������Ӧ��ͼ��Խ����Խ����x�
��4���ɺ���y= ![]() ��֪f����x��=��f��x������y=
��֪f����x��=��f��x������y= ![]() ���溯���������Ʋ������Ӧ��ͼ�����ԭ��Գƣ� ����������ʣ����������y=
���溯���������Ʋ������Ӧ��ͼ�����ԭ��Գƣ� ����������ʣ����������y= ![]() ��Ӧ��ͼ����ͼ��ʾ�����������о��У����Ǽ��õ��˴����һ���˼�룬���õ��˷������۵�˼�룬�Ƚ����˾�̬������㣩���о����ֽ����˶�̬�������ԣ���˼����������������ѧ�о��Ĺ��̣������о���ѧ�ijɹ���
��Ӧ��ͼ����ͼ��ʾ�����������о��У����Ǽ��õ��˴����һ���˼�룬���õ��˷������۵�˼�룬�Ƚ����˾�̬������㣩���о����ֽ����˶�̬�������ԣ���˼����������������ѧ�о��Ĺ��̣������о���ѧ�ijɹ���
���𰸡�
��1���⣺��y=x2�� ![]() �У�x��0�������Ʋ������Ӧ��ͼ����y�ᣬ����y��ཻ��
�У�x��0�������Ʋ������Ӧ��ͼ����y�ᣬ����y��ཻ��
��2���⣺��y=0����x2�� ![]() =0�����x=��1�������Ʋ������Ӧ��ͼ����x�ཻ����������Ϊ��1��0���ͣ���1��0����
=0�����x=��1�������Ʋ������Ӧ��ͼ����x�ཻ����������Ϊ��1��0���ͣ���1��0����
��3���⣺��y=x2�� ![]() �У���0��x��1ʱ��
�У���0��x��1ʱ�� ![]() ��1��x2����y��0����x��1ʱ��
��1��x2����y��0����x��1ʱ�� ![]() ��1��x2����y��0�������Ʋ������Ӧ��ͼ�������䣨0��1����ͼ����x����·��������䣨1��+�ޣ���ͼ����x����Ϸ�
��1��x2����y��0�������Ʋ������Ӧ��ͼ�������䣨0��1����ͼ����x����·��������䣨1��+�ޣ���ͼ����x����Ϸ�
��4���⣺��y=x2�� ![]() �У���x�ʣ�0��+�ޣ�����
�У���x�ʣ�0��+�ޣ�����
��x������ʱ ![]() ��С��x2��
��С��x2�� ![]() ��������y����������ԭ�����ڣ�0��+�ޣ�����������
��������y����������ԭ�����ڣ�0��+�ޣ�����������
�����Ʋ������Ӧ��ͼ��Խ���������ߣ��ǵ�������������
�ɺ���y=x2�� ![]() ��֪f����x��=f��x����������Ϊż�����������Ʋ������Ӧ��ͼ�����y��Գ�
��֪f����x��=f��x����������Ϊż�����������Ʋ������Ӧ��ͼ�����y��Գ�
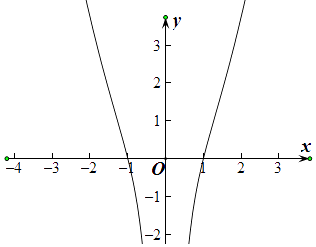
��������ͨ�������Ķ���������x�Ľ��������yֵ�ı仯���ƣ���������ż�Ժͺ����ĵ����ԣ����ɺ��������ʼ��ɣ�





