题目内容
17.定积分${∫}_{0}^{1}$[$\sqrt{1{-(x-1)}^{2}}$-x]dx等于( )| A. | $\frac{π-2}{4}$ | B. | $\frac{π}{2}$-1 | C. | $\frac{π-1}{4}$ | D. | $\frac{π-1}{2}$ |
分析 根据积分的几何意义和积分公式进行计算即可得到结论.
解答 解:${∫}_{0}^{1}$$\sqrt{1{-(x-1)}^{2}}$dx表示以(1,0)为圆心,半径r=1的圆的面积的四分之一,故${∫}_{0}^{1}$$\sqrt{1-(x-1)2}$dx=$\frac{π}{4}$,
${∫}_{0}^{1}$xdx=$\frac{1}{2}{x}^{2}$|${\;}_{0}^{1}$=$\frac{1}{2}$,
故定积分${∫}_{0}^{1}$[$\sqrt{1{-(x-1)}^{2}}$-x]dx=$\frac{π}{4}$-$\frac{1}{2}$,
故选:A
点评 本题主要考查积分的计算,要求熟练掌握常见函数的积分公式,对于不好求出的积分,要转化为求对应图形的面积.

练习册系列答案
相关题目
6.某几何体的三视图如图所示,且该几何体的体积是3,则正视图中的x的值( )
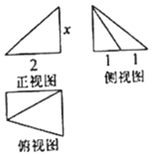

| A. | 2 | B. | 3 | C. | $\frac{3}{2}$ | D. | $\frac{9}{2}$ |
2.已知xy>0,若x2+4y2>(m2+3m)xy恒成立,则实数m的取值范围是( )
| A. | (-∞,-4]∪[-1,+∞) | B. | (-∞,-1]∪[4,+∞) | C. | (-4,1) | D. | (-1,4) |
6.设函数f(x),若对于在定义域内存在实数x满足f(-x)=-f(x),则称函数f(x)为“局部奇函数”.若函数f(x)=4x-m•2x+m2-3是定义在R上的“局部奇函数”,则实数m的取值范围是( )
| A. | [1-$\sqrt{3}$,1+$\sqrt{3}$) | B. | [-1,2) | C. | [-2$\sqrt{2}$,2$\sqrt{2}$] | D. | [-2$\sqrt{2}$,1-$\sqrt{3}$] |
7.已知$\overrightarrow{AB}$=(3,1),向量$\overrightarrow{AC}$=(-4,-3),则向量$\overrightarrow{BC}$=( )
| A. | (-7,-4) | B. | (7,4) | C. | (-1,4) | D. | (1,4) |
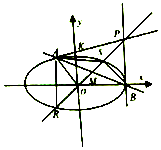 中心在原点,焦点在x轴上的椭圆C过点K(0,$\sqrt{2}$),离心率e=$\frac{\sqrt{2}}{2}$,点M($\frac{2}{3}$,$\frac{2}{3}$)在椭圆C内,椭圆C上两点A,B满足$\overrightarrow{AM}$=$\overrightarrow{MB}$.
中心在原点,焦点在x轴上的椭圆C过点K(0,$\sqrt{2}$),离心率e=$\frac{\sqrt{2}}{2}$,点M($\frac{2}{3}$,$\frac{2}{3}$)在椭圆C内,椭圆C上两点A,B满足$\overrightarrow{AM}$=$\overrightarrow{MB}$.