题目内容
 如图,多面体是由底面为ABCD的长方体被截面AEFG所截而得,其中AB=4,BC=1,BE=3,CF=4.
如图,多面体是由底面为ABCD的长方体被截面AEFG所截而得,其中AB=4,BC=1,BE=3,CF=4.(1)求
| EF |
(2)求GE与平面ABCD所成的角的正弦值;
(3)求点C到截面AEFG的距离.
分析:(1)用坐标表示点,进而可求求
,利用
=
,可求点G的坐标;
(2)求出平面ABCD的法向量,进而向量的夹角公式,可求GE与平面ABCD所成的角的正弦值;
(3)求出平面AEFG的法向量,再利用点到面的距离公式,即可求得点C到截面AEFG的距离.
| EF |
| AG |
| EF |
(2)求出平面ABCD的法向量,进而向量的夹角公式,可求GE与平面ABCD所成的角的正弦值;
(3)求出平面AEFG的法向量,再利用点到面的距离公式,即可求得点C到截面AEFG的距离.
解答:解:(1)由图可知:A(1,0,0),B(1,4,0),E(1,4,3),F(0,4,4)
∴
=(-1, 0, 1)
又∵
=
,设G(0,0,z),
则(-1,0,z)=(-1,0,1)
∴z=1,∴G(0,0,1)
(2)平面ABCD的法向量
=(0, 0, 1).
=(1, 4, 2),
设GE与平面ABCD成角为θ,则sinθ=cos(
-θ)=
=
(3)设
⊥面AEFG,
=(x0,y0,z0)
∵
⊥
,
⊥
,而
=(-1,0,1),
=(0,4,3)
∴
∴
∴
=(z0,-
z0,z0)
取z0=4,则
=(4,-3,4)
∵
=(0,0,4)
∴d=
=
即点C到截面AEFG的距离为
.
∴
| EF |
又∵
| AG |
| EF |
则(-1,0,z)=(-1,0,1)
∴z=1,∴G(0,0,1)
(2)平面ABCD的法向量
| DG |
| GE |
设GE与平面ABCD成角为θ,则sinθ=cos(
| π |
| 2 |
| ||||
|
|
2
| ||
| 21 |
(3)设
| n 0 |
| n 0 |
∵
| n 0 |
| AG |
| n 0 |
| AE |
| AG |
| AE |
∴
|
∴
|
∴
| n0 |
| 3 |
| 4 |
取z0=4,则
| n 0 |
∵
| CF |
∴d=
|
| ||||
|
|
16
| ||
| 41 |
即点C到截面AEFG的距离为
16
| ||
| 41 |
点评:本题重点考查利用向量知识解决立体几何问题,考查线面角,考查点到面的距离,求出平面的法向量是解题的关键.

练习册系列答案
相关题目
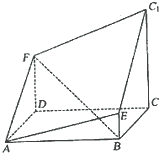 如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1.
如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1. 如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1.
如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1. 如图,多面体是由底面为ABCD的长方体被截面AEFG所截而得,其中AB=4,BC=1,BE=3,CF=4.
如图,多面体是由底面为ABCD的长方体被截面AEFG所截而得,其中AB=4,BC=1,BE=3,CF=4.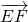 和点G的坐标;
和点G的坐标; 和点G的坐标;
和点G的坐标;