题目内容
20.已知两点A(-1,0)、B(1,0),点P(x,y)是直角坐标平面上的动点,若将点P的横坐标保持不变、纵坐标扩大到$\sqrt{2}$倍后得到点$Q(x,\sqrt{2}y)$满足$\overrightarrow{AQ}•\overrightarrow{BQ}=1$.(1)求动点P所在曲线C的轨迹方程;
(2)过点B作斜率为$-\frac{{\sqrt{2}}}{2}$的直线l交曲线C于M、N两点,且满足$\overrightarrow{OM}+\overrightarrow{ON}+\overrightarrow{OH}=\overrightarrow 0$,又点H关于原点O的对称点为点G,
①求点H,G的坐标;
②试问四点M、G、N、H是否共圆,若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
分析 (1)通过已知条件可得$\overrightarrow{AQ}=(x+1,\sqrt{2}y),\overrightarrow{BQ}=(x-1,\sqrt{2}y)$,利用$\overrightarrow{AQ}•\overrightarrow{BQ}=1$,计算即可;
(2)①联立直线l与曲线C的方程,利用韦达定理及$\overrightarrow{OM}+\overrightarrow{ON}+\overrightarrow{OH}=\overrightarrow 0$计算即可;②联立线段MN、GH的中垂线可得交点坐标,通过计算交点到M、H的距离即可得出结论.
解答 解:(1)依据题意,有$\overrightarrow{AQ}=(x+1,\sqrt{2}y),\overrightarrow{BQ}=(x-1,\sqrt{2}y)$.
∵$\overrightarrow{AQ}•\overrightarrow{BQ}=1$,∴x2-1+2y2=1.
∴动点P所在曲线C的轨迹方程是$\frac{x^2}{2}+{y^2}=1$;
(2)①∵直线l过点B,且斜率为$k=-\frac{{\sqrt{2}}}{2}$,
∴$l:y=-\frac{{\sqrt{2}}}{2}(x-1)$,
联立方程组$\left\{\begin{array}{l}\frac{x^2}{2}+{y^2}=1\\ y=-\frac{{\sqrt{2}}}{2}(x-1)\end{array}\right.$,得2x2-2x-1=0.
设两曲线的交点为M(x1,y1)、N(x2,y2),
由韦达定理,可得:$\left\{\begin{array}{l}{x_1}+{x_2}=1\\{y_1}+{y_2}=\frac{{\sqrt{2}}}{2}\end{array}\right.$.
又∵$\overrightarrow{OM}+\overrightarrow{ON}+\overrightarrow{OH}=\overrightarrow 0$,
∴$\left\{\begin{array}{l}{{x}_{G}+{x}_{1}+{x}_{2}=0}\\{{y}_{G}+{y}_{1}+{y}_{2}=0}\end{array}\right.$,∴xG=-1,yG=-$\frac{\sqrt{2}}{2}$,
又点G与点H关于原点对称,
于是可得点$H(-1,-\frac{{\sqrt{2}}}{2})$、$G(1,\frac{{\sqrt{2}}}{2})$.
②结论:四点M、G、N、H共圆,圆心坐标为${O_1}(\frac{1}{8},-\frac{{\sqrt{2}}}{8})$,半径为$\frac{{3\sqrt{11}}}{8}$.
理由如下:
若线段MN、GH的中垂线分别为l1和l2,则有${l_1}:y-\frac{{\sqrt{2}}}{4}=\sqrt{2}(x-\frac{1}{2})$,${l_2}:y=-\sqrt{2}x$.
联立方程组$\left\{\begin{array}{l}y-\frac{{\sqrt{2}}}{4}=\sqrt{2}(x-\frac{1}{2})\\ y=-\sqrt{2}x\end{array}\right.$,解得l1和l2的交点为${O_1}(\frac{1}{8},-\frac{{\sqrt{2}}}{8})$.
因此,可算得$|{O_1}H|=\sqrt{{{(\frac{9}{8})}^2}+{{(\frac{{3\sqrt{2}}}{8})}^2}}=\frac{{3\sqrt{11}}}{8}$,$|{O_1}M|=\sqrt{{{({x_1}-\frac{1}{8})}^2}+{{({y_1}+\frac{{\sqrt{2}}}{8})}^2}}=\frac{{3\sqrt{11}}}{8}$.
所以,四点M、G、N、H共圆,圆心坐标为${O_1}(\frac{1}{8},-\frac{{\sqrt{2}}}{8})$,半径为$\frac{{3\sqrt{11}}}{8}$.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,涉及到韦达定理、向量的坐标运算、两点间距离公式等基础知识,注意解题方法的积累,属于中档题.

| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
90 89 90 95 93 94 93
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为( )
| A. | 92,2 | B. | 92,2.8 | C. | 93,2 | D. | 93,2.8 |
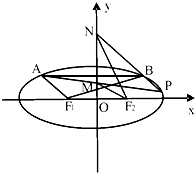 如图,F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且焦距为2$\sqrt{2}$,动弦AB平行于x轴,且|F1A|+|F2A|=4.
如图,F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且焦距为2$\sqrt{2}$,动弦AB平行于x轴,且|F1A|+|F2A|=4. 中,
中, 底面
底面 ,底面
,底面 是直角梯形,
是直角梯形, .
.
 上确定一点
上确定一点 ,使得
,使得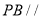 平面
平面 ,并求
,并求 的值;
的值; 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值. 是虚数单位,若复数
是虚数单位,若复数 在复平面内对应的点在第四象限,则实数
在复平面内对应的点在第四象限,则实数 的值可能是( )
的值可能是( )