题目内容
(本小题满分12分)
(注意:在试题卷上作答无效)
设函数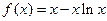 .数列
.数列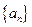 满足
满足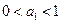 ,
,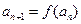 .
.
(Ⅰ)证明:函数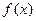 在区间
在区间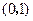 是增函数;
是增函数;
(Ⅱ)证明: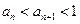 ;
;
(Ⅲ)设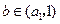 ,整数
,整数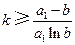 .证明:
.证明: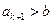 .
.
(注意:在试题卷上作答无效)
设函数
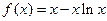 .数列
.数列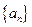 满足
满足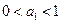 ,
,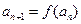 .
.(Ⅰ)证明:函数
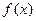 在区间
在区间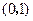 是增函数;
是增函数;(Ⅱ)证明:
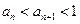 ;
;(Ⅲ)设
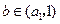 ,整数
,整数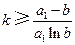 .证明:
.证明: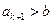 .
.(Ⅰ)证明见解析。
(Ⅱ)证明见解析。
(Ⅲ)证明见解析。
(Ⅱ)证明见解析。
(Ⅲ)证明见解析。
(Ⅰ)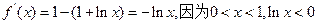 ,
,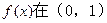 上为增函数
上为增函数
(Ⅱ)当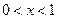 时,
时,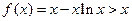 ,又由(Ⅰ)及
,又由(Ⅰ)及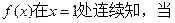
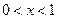 时,
时,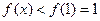 ,因此当
,因此当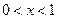 时,
时, 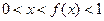 ①
①
下面运用数学归纳法可以证明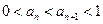 ②
②
(ⅰ)由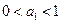 ,
,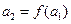 ,应用式①得当
,应用式①得当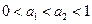 ,即得当
,即得当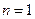 时,不等式②成立.
时,不等式②成立.
(ⅱ)假设当 时,不等式②成立,即
时,不等式②成立,即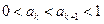 ,则由①可得
,则由①可得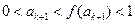 ,即
,即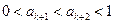 ,故当
,故当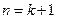 时,不等式②成立
时,不等式②成立
综合(ⅰ)(ⅱ)证得,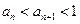
(Ⅲ)由(Ⅱ)知,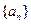 逐项递增,故若存在正整数
逐项递增,故若存在正整数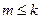 ,使得
,使得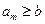 ,则
,则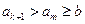 ,否则若
,否则若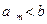
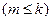 ,则由
,则由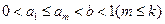 知,
知,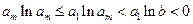 ③
③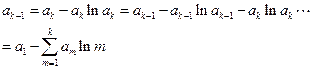 由③知
由③知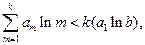
于是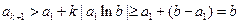
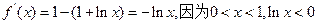 ,
,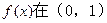 上为增函数
上为增函数(Ⅱ)当
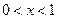 时,
时,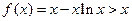 ,又由(Ⅰ)及
,又由(Ⅰ)及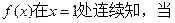
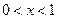 时,
时,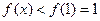 ,因此当
,因此当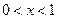 时,
时, 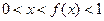 ①
①下面运用数学归纳法可以证明
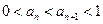 ②
②(ⅰ)由
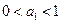 ,
,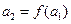 ,应用式①得当
,应用式①得当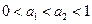 ,即得当
,即得当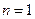 时,不等式②成立.
时,不等式②成立.(ⅱ)假设当
 时,不等式②成立,即
时,不等式②成立,即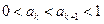 ,则由①可得
,则由①可得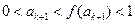 ,即
,即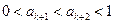 ,故当
,故当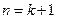 时,不等式②成立
时,不等式②成立综合(ⅰ)(ⅱ)证得,
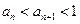
(Ⅲ)由(Ⅱ)知,
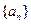 逐项递增,故若存在正整数
逐项递增,故若存在正整数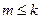 ,使得
,使得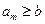 ,则
,则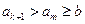 ,否则若
,否则若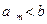
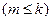 ,则由
,则由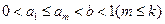 知,
知,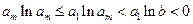 ③
③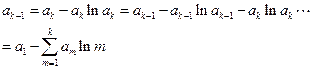 由③知
由③知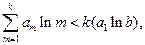
于是
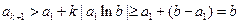

练习册系列答案
相关题目
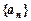 是等差数列,
是等差数列,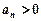 ,公差
,公差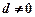 ,求证:
,求证: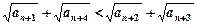
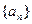 满足:
满足: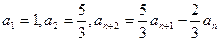 ,(n=1,2,…)。
,(n=1,2,…)。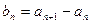 ,(n=1,2,…)。求数列
,(n=1,2,…)。求数列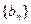 的通项公式;(2)求数列
的通项公式;(2)求数列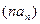 的前n项和Sn。
的前n项和Sn。
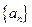 为等比数列,
为等比数列,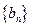 为等差数列,且
为等差数列,且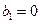 ,
,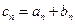 ,若数列
,若数列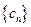 是1,1,2,…,则数列
是1,1,2,…,则数列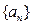 中,
中,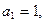 点
点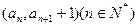 在函数
在函数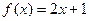 的图像上,
的图像上,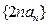 的前n项和
的前n项和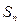 .
. 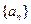 的前
的前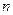 项和为
项和为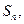 且
且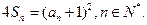
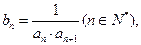 求数列
求数列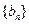 的前
的前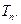
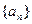 满足
满足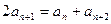
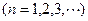 ,它的前
,它的前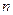 项和为
项和为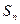 ,且
,且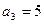 ,
,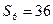 .(1)求
.(1)求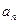 ;(2)已知等比数列
;(2)已知等比数列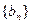 满足
满足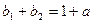 ,
,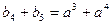
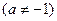 ,设数列
,设数列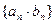 的前
的前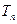 ,求
,求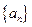 为等差数列,首项
为等差数列,首项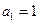 ,公差
,公差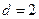 ,
,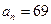 ,则
,则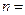 ( )
( )