题目内容
【题目】已知椭圆![]() :
:![]() 的左焦点为
的左焦点为![]() ,设
,设![]() 是椭圆
是椭圆![]() 的两个短轴端点,
的两个短轴端点,![]() 是椭圆
是椭圆![]() 的长轴左端点.
的长轴左端点.
(Ⅰ)当![]() 时,设点
时,设点![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,且直线
,且直线![]() 的斜率分别为
的斜率分别为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)当![]() 时,若经过
时,若经过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,O为坐标原点,求
两点,O为坐标原点,求![]() 与
与![]() 的面积之差的最大值.
的面积之差的最大值.
【答案】见解析
【解析】(Ⅰ)由条件,不妨设![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]() ,…1分
,…1分
所以直线![]() 的方程为
的方程为![]() ,代入
,代入![]() ,得
,得![]() ,
,
解得![]() ,所以
,所以![]() ,
,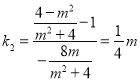 ,……4分
,……4分
所以![]() . ………………5分
. ………………5分
(Ⅱ)设![]() 与
与![]() 的面积分别为
的面积分别为![]() ,
,
当直线![]() 的斜率不存在时,直线方程为
的斜率不存在时,直线方程为![]() ,此时不妨设
,此时不妨设![]() ,则
,则![]() ,
,![]() 的面积相等,即
的面积相等,即![]() .………………6分
.………………6分
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,设
,设![]() ,
,
和椭圆方程联立得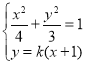 ,消掉
,消掉![]() 得
得![]() ,………………7分
,………………7分
显然![]() ,方程有实根,且
,方程有实根,且![]() .………………8分
.………………8分
此时![]()
![]() .
.
因为![]() ,上式
,上式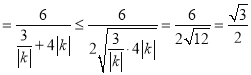 (当且仅当
(当且仅当![]() 时等号成立),
时等号成立),
所以![]() 的最大值为
的最大值为![]() .………………12分
.………………12分
【命题意图】本题考查椭圆的方程与几何性质、直线斜率、直线与椭圆的位置关系,以及考查逻辑思维能
力、分析与解决问题的综合能力、运算求解能力、方程思想与分类讨论的思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目