题目内容
在半径为常量r，圆心角为变量2α（0°＜2α＜180°）的扇形OAB内做一内切圆p，再在扇形内作一个扇形两半径相切并与圆p外切的小圆q，求圆q半径的最大值．
分析：设圆q半径为x，圆p半径为y，则由三角形相似可得
=
，求出x，利用配方法，即可求圆q半径的最大值．
| x |
| y |
| r-x-2y |
| r-y |
解答：
解：设圆q半径为x，圆p半径为y，则
由三角形相似可得
=
，
∴x=-
y2+y=-
（y-
）2+
，
∴y=
时，圆q半径的最大值为
．
解：设圆q半径为x，圆p半径为y，则由三角形相似可得
| x |
| y |
| r-x-2y |
| r-y |
∴x=-
| 2 |
| r |
| 2 |
| r |
| r |
| 4 |
| r |
| 8 |
∴y=
| r |
| 4 |
| r |
| 8 |
点评：本题考查扇形OAB内做一内切圆，考查三角形相似，考查配方法的运用，属于中档题．
练习册系列答案
相关题目
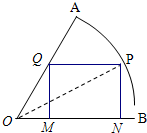如图，在半径为R、圆心角为60°的扇形AB弧上任取一点P，作扇形的内接矩形PNMQ，使点Q在OA上，点M，N在OB上，设∠BOP=θ，矩形PNMQ的面积记为S．
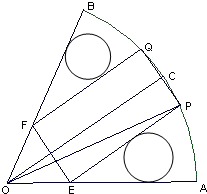如图，在半径为R、圆心角为
有一块扇形铁板，半径为R，圆心角为60°，从这个扇形中切割下一个内接矩形，即矩形的各个顶点都在扇形的半径或弧上（如图所示），求这个内接矩形的最大面积．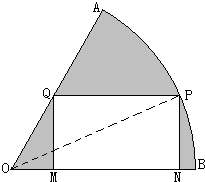
如图，在半径为R、圆心角为