题目内容
等比数列{an}的前三项和S3=18,若a1,3-a2,a3成等差数列,则公比q=( )A.2或
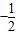
B.-2或

C.-2或
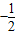
D.2或

【答案】分析:设出等比数列的公比,根据题意列关于a1和q方程组,求解方程组即可得到答案.
解答:解:设等比数列的公比为q,由a1,3-a2,a3成等差数列,
所以2(3-a2)=a1+a3,即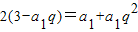 ①,
①,
又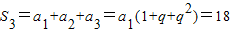 ②,
②,
由①得: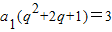 ③,
③,
③÷②得: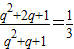 ,解得:q=-2或q=-
,解得:q=-2或q=- .
.
故选C.
点评:本题考查了等比数列的通项公式,考查方程组的求解方法,此题是基础题,是会考常见题型.
解答:解:设等比数列的公比为q,由a1,3-a2,a3成等差数列,
所以2(3-a2)=a1+a3,即
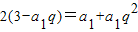 ①,
①,又
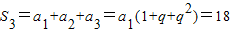 ②,
②,由①得:
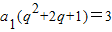 ③,
③,③÷②得:
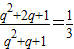 ,解得:q=-2或q=-
,解得:q=-2或q=- .
.故选C.
点评:本题考查了等比数列的通项公式,考查方程组的求解方法,此题是基础题,是会考常见题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012•蓝山县模拟)统计某校高三年级100名学生的数学月考成绩,得到样本频率分布直方图如下图所示,已知前4组的频数分别是等比数列{an}的前4项,后6组的频数分别是等差数列{bn}的前6项,
(2012•蓝山县模拟)统计某校高三年级100名学生的数学月考成绩,得到样本频率分布直方图如下图所示,已知前4组的频数分别是等比数列{an}的前4项,后6组的频数分别是等差数列{bn}的前6项,