题目内容
已知曲线![]() 〉在点(t,
〉在点(t,![]() >处的切线Z交X轴于点A,交:y轴于点
>处的切线Z交X轴于点A,交:y轴于点![]() (O为坐标原点)的面积为S.
(O为坐标原点)的面积为S.
(I)试写出S关于r的函数关系式,
(II)求面积s的最小值;
(III)若![]() 对于
对于![]() •恒成立,求实数a的取值范围.
•恒成立,求实数a的取值范围.
解:⑴曲线![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() ,--------1分
,--------1分
设![]() ,
,
则![]() ----------- 2分
----------- 2分
解得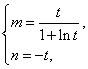
所以![]() ,注意到
,注意到![]() 时,
时,![]() ,
,
故![]() 为所求.------------------- 4分
为所求.------------------- 4分
⑵记![]() ,则
,则![]() ,
,
![]() 时,
时,![]() ;
;
![]() 时,
时,![]() ,
,
即函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,------ 6分
上单调递增,------ 6分
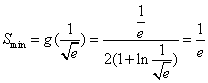 ,
,
所以面积![]() 的最小值为
的最小值为![]() ,当且仅当
,当且仅当![]() 时取到.------------------- 8分
时取到.------------------- 8分
⑶由![]() ,及
,及![]() 得,
得,![]() 对
对![]() 恒成立.
恒成立.
记![]() ,则
,则![]() ,
,
当![]() ,即
,即![]() 或
或![]() 时,
时,![]() 恒成立,
恒成立,
此时![]() 在
在![]() 上单调递增,
上单调递增,
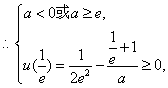 ----------- 10分
----------- 10分
解得![]() ,
,
当![]() ,即
,即![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
此时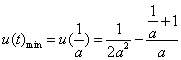 ,
,
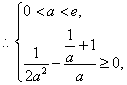 解得
解得![]() ,
,
综上,![]() 为所求.------------------- 12分
为所求.------------------- 12分

练习册系列答案
相关题目
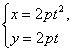 (t为参数),点A、B在曲线上对应的参数分别为t1和t2,又t1+t2=0,则|AB|等于( )
(t为参数),点A、B在曲线上对应的参数分别为t1和t2,又t1+t2=0,则|AB|等于( )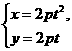 (t为参数),点A、B在曲线上对应的参数分别为t1和t2,又t1+t2=0,则|AB|等于( )
(t为参数),点A、B在曲线上对应的参数分别为t1和t2,又t1+t2=0,则|AB|等于( )