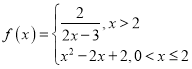Question

【题目】已知是定义在上的偶函数，满足，当时，，若，，，则，，的大小关系为（ ）

A.B.C.D.

Answer 1

【答案】B

【解析】

根据题意，分析可得函数f（x）是周期为2的周期函数，据此可得c＝f（2019）＝f（1+2×1007）＝f（1），b＝f（log24.1）＝f（log24.1﹣2）＝f（log2），结合函数的奇偶性可得a=f（log2）＝f（﹣log2）＝f（log2），结合函数解析式可得f（x）在[0，1]上为增函数，据此分析可得答案．

根据题意，f（x）满足f（x+2）＝f（x），即函数f（x）是周期为2的周期函数，

则c＝f（2019）＝f（1+2×1009）＝f（1），b＝f（log24.1）＝f（log24.1﹣2）＝f（log2），

又由f（x）为偶函数，则a=f（log2）＝f（﹣log2）＝f（log2），

当x∈[0，1]时，f（x）＝x3+x，易得f（x）在[0，1]上为增函数，又由0＜log2log21，

则有b＜a＜c；

故选：B．